
【题目】如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
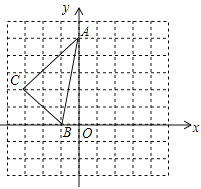
(1)画出将△ABC向右平移2个单位得到△A1B1C1;
(2)画出将△ABC绕点O顺时针方向旋转90°得到的△A2B2C2;
(3)求△A1B1C1与△A2B2C2重合部分的面积.
【答案】(1)作图见解析;(2)作图见解析;(3)![]() .
.
【解析】
试题分析:(1)将△ABC向右平移2个单位即可得到△A1B1C1.
(2)将△ABC绕点O顺时针方向旋转90°即可得到的△A2B2C2.
(3)B2C2与A1B1相交于点E,B2A2与A1B1相交于点F,如图,求出直线A1B1,B2C2,A2B2,列出方程组求出点E、F坐标即可解决问题.
试题解析:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;
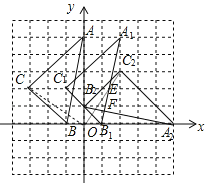
(3)B2C2与A1B1相交于点E,B2A2与A1B1相交于点F,如图,∵B2(0,1),C2(2,3),B1(1,0),A1(2,5),A2(5,0),∴直线A1B1为y=5x﹣5,直线B2C2为y=x+1,直线A2B2为![]() ,由
,由![]() 解得:
解得:![]() ,∴点E(
,∴点E(![]() ,
,![]() ),由
),由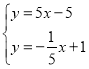 解得:
解得: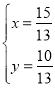 ,∴点F(
,∴点F(![]() ,
,![]() ),∴S△BEF=
),∴S△BEF=![]() =
=![]() ,∴△A1B1C1与△A2B2C2重合部分的面积为
,∴△A1B1C1与△A2B2C2重合部分的面积为![]() .
.


 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】将抛物线y=﹣2x2向右平移1个单位长度,再向上平移1个单位长度所得的抛物线解析式为( )
A. y=﹣2(x+1)2 B. y=﹣2(x+1)2+2 C. y=﹣2(x﹣1)2+2 D. y=﹣2(x﹣1)2+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某船上午11时30分在A处观测海岛B在北偏东60°方向,该船以每小时10海里的速度航行到C处,再观测海岛B在北偏东30°方向,又以同样的速度继续航行到D处,再观测海岛在北偏西30°方向,当轮船到达C处时恰好与海岛B相距20海里,请你确定轮船到达C处和D处的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解一元二次方程x2﹣6x=8时,此方程可变形为( )
A.(x﹣3)2=17
B.(x﹣3)2=1
C.(x+3)2=17
D.(x+3)2=1
查看答案和解析>>
科目:初中数学 来源: 题型:
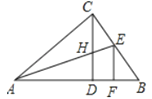
【题目】如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,角平分线AE交CD于H,EF⊥AB于F,下列结论:①∠ACD=∠B;②CH=CE=EF;③AC=AF;④CH=HD.其中正确的结论为( )
A.①②④ B.①②③ C. ②③ D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() (m<0)与x轴交于点A、B(点A在点B的左侧),该抛物线的对称轴与直线
(m<0)与x轴交于点A、B(点A在点B的左侧),该抛物线的对称轴与直线![]() 相交于点E,与x轴相交于点D,点P在直线
相交于点E,与x轴相交于点D,点P在直线![]() 上(不与原点重合),连接PD,过点P作PF⊥PD交y轴于点F,连接DF.
上(不与原点重合),连接PD,过点P作PF⊥PD交y轴于点F,连接DF.
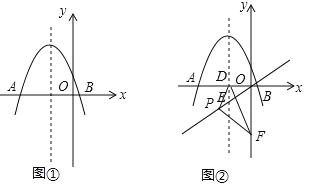
(1)如图①所示,若抛物线顶点的纵坐标为![]() ,求抛物线的解析式;
,求抛物线的解析式;
(2)求A、B两点的坐标;
(3)如图②所示,小红在探究点P的位置发现:当点P与点E重合时,∠PDF的大小为定值,进而猜想:对于直线![]() 上任意一点P(不与原点重合),∠PDF的大小为定值.请你判断该猜想是否正确,并说明理由.
上任意一点P(不与原点重合),∠PDF的大小为定值.请你判断该猜想是否正确,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
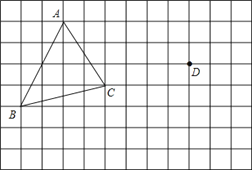
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的△DEF,并求△DEF的面积=
(2)若连接AD、CF,则这两条线段之间的关系是_________________;
(3)请在AB上找一点P,使得线段CP平分△ABC的面积,在图上作出线段CP.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com