练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
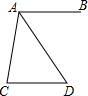
    3．如图，AB∥CD，AD平分∠BAC，且∠C=80°，求∠D的度数．

    分析 首先根据平行线的性质可知：∠D=∠BAD，∠CAB=100°，然后由角平分线的定义可知∠BAD=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×100°=50°，从而可求得∠D的度数．

    解答 解：∵AB∥CD，
    ∴∠C+∠CAB=180°，∠D=∠BAD．
    ∴∠CAB=180°-80°=100°．
    ∵AD平分∠BAC，
    ∴∠BAD=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×100°=50°，
    ∴∠D=∠BAD=50°．

    点评 本题主要考查的是平行线的性质和角平分线的定义，利用角平分线的定义和平行线的性质求得∠CAB、∠BAD的度数是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    13．临近中招，老师将小华同学“考前五套卷”数学分数统计如下：101，98，103，101，99．老师判断小华成绩还算比较稳定．老师判断的依据是（　　）
    A．众数B．平均数C．中位数D．方差

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

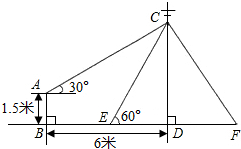    14．如图，在电线杆上的C处引拉线CE、CF固定电线杆，拉线CE和地面成60°角，在离电线杆6米的B处安置测角仪，在A处测得电线杆上C处的仰角为30°，已知测角仪高AB为1.5米，求拉线CE的长（结果保留根号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．在一次科技作品制作比赛中，某小组八件作品的成绩（单位：分）分别是 6，9，9，8，6，9，9，8，对于这组数据，下列说法不正确的是（　　）
    A．中位数是8B．众数是9C．平均数是8D．方差是1.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

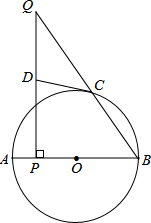    18．如图，AB是⊙O的直径，点C在⊙O上，点P是直径AB上的一点（不与A，B重合），过点P作AB的垂线交BC的延长线于点Q．
    （1）在线段PQ上取一点D，使DQ=DC，连接DC，试判断CD与⊙O的位置关系，并说明理由；
    （2）若cosB=$\frac{3}{5}$，AP=1，求QC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．下列几项调查中，适合使用普查的是（　　）
    A．调查我区奶制品中蛋白质含量是否达到国家标准
    B．调查我区6月1日这天嘉陵江水中氨氮含量是否超标
    C．调查我校初三某班全体学生的视力状况
    D．调查我区市民对消防安全知识的知晓情况

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．若一条直线将一个平面图形分成面积相等的两部分，则该直线被平面图形截得的线段叫做该图形的面径．例如圆的直径就是它的面径．

    （1）已知等边三角形的边长为2，则它的面径长可以是$\sqrt{2}，\sqrt{3}$（写出2个）；
    （2）如图1，在梯形ABCD中，AB∥DC，M是AD的中点，射线CM交射线BA于点E．取EB的中点F，连接CF．求证：CF是梯形ABCD的面径；
    （3）如图2，在Rt△ABC中，∠ABC=Rt∠，D，E分别是线段BC，AC上的点，EF是四边形ABDE的一条面径．若AB=CB=CE=2，∠BED=45°，求DF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．如图，AD∥BC，BE平分∠ABC，∠BED=145°，则∠BAD=110°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

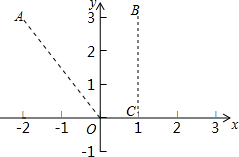    13．对于两个已知图形G1、G2，在G1上任取一点P，在G2上任取一点Q，当线段PQ的长度最小时，我们称这个最小的长度为G1、G2的“密距”．如图，A（-2，3），B（1，3），C（1，0），则点A与射线OC之间的“密距”为$\sqrt{13}$，点B与射线OC之间的“密距”为3，如果直线y=x-1和双曲线y=$\frac{k}{x}$之间的“密距”为$\frac{3\sqrt{2}}{2}$，则k的值为-4．

    查看答案和解析>>

    同步练习册答案