
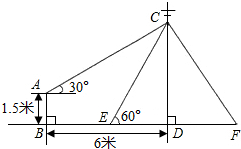
 如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).
如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号). 分析 作AG⊥CD,垂足为G.在Rt△AGC中,根据CG=AG•tan30°,求出CG的长;在Rt△CED中,根据CE=$\frac{CD}{sin60°}$,求出CE的长.
解答 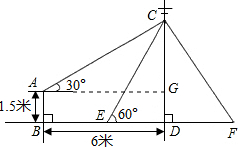 解:作AG⊥CD,垂足为G.
解:作AG⊥CD,垂足为G.
易得AG=BD,
在Rt△AGC中,CG=AG•tan30°=6×$\frac{\sqrt{3}}{3}$=2$\sqrt{3}$米,
可得CD=CG+GD=(2$\sqrt{3}$+1.5)米,
在Rt△CED中,CE=$\frac{CD}{sin60°}$=$\frac{2\sqrt{3}+1.5}{\frac{\sqrt{3}}{2}}$=(4+$\sqrt{3}$)米.
答:拉线CE的长为(4+$\sqrt{3}$)米.
点评 本题考查了解直角三角形--仰角俯角问题,熟悉三角函数和解直角三角形的应用是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
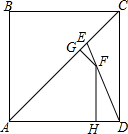 如图,已知正方形ABCD的边长为1,对角线AC上有一点E,使得AE=$\frac{{\sqrt{2}}}{2}$AC.连结DE,过线段DE上的一个动点F分别向AC和AD作垂线段,垂足分别为G、H.
如图,已知正方形ABCD的边长为1,对角线AC上有一点E,使得AE=$\frac{{\sqrt{2}}}{2}$AC.连结DE,过线段DE上的一个动点F分别向AC和AD作垂线段,垂足分别为G、H.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 小明在10次抛图钉的试验中发现3次钉尖朝上,由此他说钉尖朝上的概率是$\frac{3}{10}$ | |
| B. | 随机抛掷一枚均匀的硬币,落地后反面一定朝上 | |
| C. | 某彩票的中奖机会是2%,那么如果买100张彩票一定会有2张中奖 | |
| D. | 在一次课堂进行的抛硬币试验中,同学们估计硬币落地后正面朝上的概率为0.51 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com