
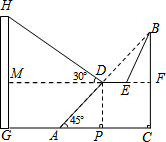
 ��ͼ��֪б��AB��60$\sqrt{2}$�ף��½ǣ�����BAC��Ϊ45�㣬BC��AC���ּƻ���б���е�D����ȥ����б�£���һ��ƽ����ˮƽ��CA������ƽ̨DE��һ���µ�б��BE����������С�������������ţ���
��ͼ��֪б��AB��60$\sqrt{2}$�ף��½ǣ�����BAC��Ϊ45�㣬BC��AC���ּƻ���б���е�D����ȥ����б�£���һ��ƽ����ˮƽ��CA������ƽ̨DE��һ���µ�б��BE����������С�������������ţ������� ��1�������Ǻ����Ķ��壬�������DF��BF�ij��������¶ȵĶ��壬�������EF�ij����̶����ƽ̨DE�ij���
��2��������GH=x�ף���x��ʾ��MH�ij�����Rt��DMH�������Ǻ����Ķ��壬���x��ֵ�����ɵõ�GH�ij���
���  �⣺��1����FM��CG��
�⣺��1����FM��CG��
���BDF=��BAC=45�㣬
��б��AB��60$\sqrt{2}$�ף�D��AB���е㣬
��BD=30$\sqrt{2}$�ף�
��DF=BD•cos��BDF=30$\sqrt{2}$��$\frac{\sqrt{2}}{2}$=30���ף���BF=DF=30�ף�
��б��BE���±�Ϊ$\sqrt{3}$��1��
��$\frac{BF}{EF}$=$\frac{\sqrt{3}}{1}$��
��ã�EF=10$\sqrt{3}$��
��DE=DF-EF=30-10$\sqrt{3}$���ף���
������ƽ̨DE�ij��ǣ�30-10$\sqrt{3}$���ף�
��2����GH=x�ף���MH=GH-GM=x-30���ף���DM=AG+AP=36+30=66���ף���
��Rt��DMH��tan30��=$\frac{MH}{DM}$����$\frac{x-30}{66}$=$\frac{\sqrt{3}}{3}$��
��ã�x=30+22$\sqrt{3}$��
�𣺽�����GH�ĸ�Ϊ��30+22$\sqrt{3}$���ף�
���� ���⿼���˽�ֱ�������ε�Ӧ��-���Ǹ������⣬�Լ���ֱ�������ε�Ӧ��-�¶��½����⣮�����ѶȽϴ�ע����������ֱ�������Σ�����ֱ�������Σ�ע���������ν��˼���뷽��˼���Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��mx=nx����m=n | |
| B�� | ��|x|-x=0����x=0 | |
| C�� | ��mx=nx���� $\frac{2m}{{x}^{2015}+1}$=$\frac{2n}{{x}^{2015}+1}$ | |
| D�� | ��m=n����24-mx=24-nx |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 21��19 | B�� | 20��19 | C�� | 19��19 | D�� | 19��22 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
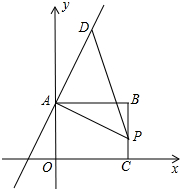 ��ͼ������ABC0λ��ֱ������ƽ�棬OΪԭ�㣬A��C�ֱ����������ϣ�B������Ϊ��8��6�����߶�BC����һ����P����֪��D�ڵ�һ���ޣ�
��ͼ������ABC0λ��ֱ������ƽ�棬OΪԭ�㣬A��C�ֱ����������ϣ�B������Ϊ��8��6�����߶�BC����һ����P����֪��D�ڵ�һ���ޣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ƽ������5 | B�� | ������5 | C�� | ������5 | D�� | ��λ����7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��Ȼ�¼��ĸ���Ϊ1 | |
| B�� | ����6��4��2��2��1��ƽ������3 | |
| C�� | ����5��2��-3��0��3�������2 | |
| D�� | ij����Ϸ����н���Ϊ20%����ô�μ����ֻ100�α���20���н� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
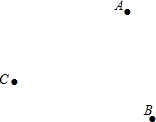 ��ͼ����֪��A��B��C����ͬһֱ���ϣ���������䣬���Ҫ��
��ͼ����֪��A��B��C����ͬһֱ���ϣ���������䣬���Ҫ���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com