
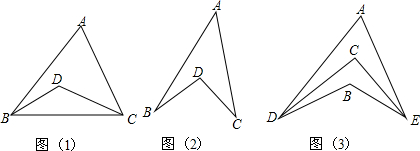
分析 (1)先根据三角形内角和定理求出∠ACB+∠ABC的度数,由∠ABD=20°,∠ACD=35°求出∠DBC+∠DCB的度数,再根据三角形内角和等于180°即可得出结论;
(2)连接BC,由三角形内角和定理可得出∠A+∠ABD+∠ACD=180°-∠DBC-∠BCD,同理,在△DBC中∠BDC=180°-∠DBC-∠BCD,由此即可得出结论;
(3)先根据∠DAE=50°,∠DBE=130°得出∠ADB+∠AEB=80°,再由DC平分∠ADB,EC平分∠AEB可知∠ADC=$\frac{1}{2}$∠ADB,∠AEC=$\frac{1}{2}$∠AEB,故可得出∠ADC+∠AEC=$\frac{1}{2}$(∠ADB+∠AEB)=40°,∠DCE=∠A+∠ADC+∠AEC=50°+40°=90°.
解答 解:(1)∵∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°-62°=118°,
∵∠ABD=20°,∠ACD=35°,
∴∠DBC+∠DCB=118°-20°-35°=63°,
∴∠BDC=180°-(∠DBC+∠DCB)=117°;
(2)∠BDC=∠A+∠B+∠C,
理由:连接BC,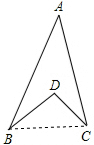 ∵∠A+∠ABD+∠DBC+∠ACD+∠BCD=180°,
∵∠A+∠ABD+∠DBC+∠ACD+∠BCD=180°,
∴∠A+∠ABD+∠ACD=180°-∠DBC-∠BCD,
∵∠BDC+∠DBC+∠BCD=180°,
∴∠BDC=180°-∠DBC-∠BCD,
∴∠BDC=∠A+∠B+∠C;
(3)∵∠DAE=50°,∠DBE=130°,
∴∠ADB+∠AEB=80°,
∵DC平分∠ADB,EC平分∠AEB,
∴∠ADC=$\frac{1}{2}$∠ADB,∠AEC=$\frac{1}{2}$∠AEB,
∴∠ADC+∠AEC=$\frac{1}{2}$(∠ADB+∠AEB)=40°,
∴∠DCE=∠A+∠ADC+∠AEC=50°+40°=90°.
点评 本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键,注意角平分线的定义的正确运用.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 25π | B. | $\frac{25}{4}$π | C. | $\frac{25}{2}$π | D. | $\frac{13}{2}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
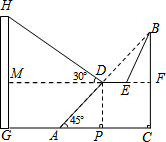 如图已知斜坡AB长60$\sqrt{2}$米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(下面两个小题结果都保留根号).
如图已知斜坡AB长60$\sqrt{2}$米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(下面两个小题结果都保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
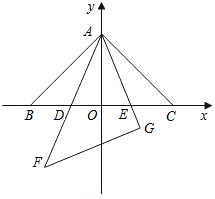 如图,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2,若△ABC固定不动,△AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n.下列结论:
如图,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2,若△ABC固定不动,△AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n.下列结论:| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com