
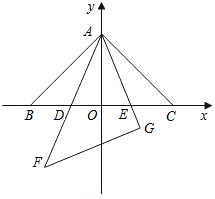
 ��ͼ����ͬһƽ���ڣ�������ȫ�ȵĵ���ֱ��������ABC��AFG�ڷ���һ��AΪ�������㣬��BAC=��AGF=90�㣬���ǵ�б�߳�Ϊ2������ABC�̶���������AFG�Ƶ�A��ת��AF��AG���BC�Ľ���ֱ�ΪD��E����D�����B�غϣ���E�����C�غϣ�����BE=m��CD=n�����н��ۣ�
��ͼ����ͬһƽ���ڣ�������ȫ�ȵĵ���ֱ��������ABC��AFG�ڷ���һ��AΪ�������㣬��BAC=��AGF=90�㣬���ǵ�б�߳�Ϊ2������ABC�̶���������AFG�Ƶ�A��ת��AF��AG���BC�Ľ���ֱ�ΪD��E����D�����B�غϣ���E�����C�غϣ�����BE=m��CD=n�����н��ۣ�| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
���� ��1��������֪�����������ε��ж��������з������ɣ�
��2���ɸ��ݣ�1���е�����������BAE��CDA�ó�����AB��BE��CD��AC�ı�����ϵ��AB��AC��ͨ������ֱ���������������˸��ݱ�����ϵ���ɵó�m��n�ĺ�����ϵʽ��
��3��������ת�ǣ�����֪��HB��BD����ôDH2=BH2+BD2����BH=CE�����ǹؼ���֤��HD=DE������AH��DH��ô��ͨ��֤������AHD��ADEȫ������⣮
��4������ABC�̶���������AFG�Ƶ�A��ת���õ���BAD�١�CAE�����ǡ�ABD���ACE��һ��ȫ�ȣ�
��5����AF��AB�غ�ʱ��AE=$\frac{1}{2}$AF��AB=$\frac{\sqrt{2}}{2}$AF���õ�DF$��\frac{1}{2}$AF��������AE��DF��һ����ȣ�
���  �⣺��1���ߡ�ABE�ס�DAE����ABE�ס�DCA��
�⣺��1���ߡ�ABE�ס�DAE����ABE�ס�DCA��
���DAE�ס�DCA����ABO�ס�ABC��
��ͼ�����������ƶ���ȫ�ȵ������Σ��ʣ�1����ȷ��
��2���ߡ�ABE�ס�DCA��
��$\frac{BE}{AC}$=$\frac{BA}{CD}$��
�������֪CA=BA=$\sqrt{2}$��
��$\frac{m}{\sqrt{2}}$=$\frac{\sqrt{2}}{n}$��
��m=$\frac{2}{n}$��
��mn=2����1��n��2����
�ʣ�2����ȷ��
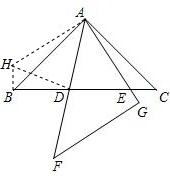
��3��֤��������ACE�Ƶ�A˳ʱ����ת90������ABH��λ�ã���CE=HB��AE=AH��
��ABH=��C=45�㣬��ת�ǡ�EAH=90�㣮
����HD���ڡ�EAD�͡�HAD�У�
��AE=AH����HAD=��EAH-��FAG=45��=��EAD��AD=AD��
���EAD�ա�HAD��
��DH=DE��
�֡�HBD=��ABH+��ABD=90�㣬
��BD2+CE2=DH2��
��BD2+CE2=DE2��
�ʣ�3����ȷ��
��4������ABC�̶���������AFG�Ƶ�A��ת��
���BAD�١�CAE��
���ABD���ACE��һ��ȫ�ȣ�
�ࣨ4������
��5����AF��AB�غ�ʱ��
AE=$\frac{1}{2}$AF��AB=$\frac{\sqrt{2}}{2}$AF��
��DF$��\frac{1}{2}$AF��
��AE��DF��һ����ȣ�
�ࣨ5������
��ѡB��
���� ������Ҫ�����˵���ֱ�������ε����ʣ����������κ�ȫ�������ε��ж������ʵ�֪ʶ����ۺ����ã��������������λ�ȫ�������εó��߶γɱ���������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
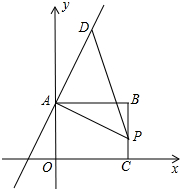 ��ͼ������ABC0λ��ֱ������ƽ�棬OΪԭ�㣬A��C�ֱ����������ϣ�B������Ϊ��8��6�����߶�BC����һ����P����֪��D�ڵ�һ���ޣ�
��ͼ������ABC0λ��ֱ������ƽ�棬OΪԭ�㣬A��C�ֱ����������ϣ�B������Ϊ��8��6�����߶�BC����һ����P����֪��D�ڵ�һ���ޣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��Ȼ�¼��ĸ���Ϊ1 | |
| B�� | ����6��4��2��2��1��ƽ������3 | |
| C�� | ����5��2��-3��0��3�������2 | |
| D�� | ij����Ϸ����н���Ϊ20%����ô�μ����ֻ100�α���20���н� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x-3��2=6 | B�� | ��x-3��2=3 | C�� | ��x-3��2=0 | D�� | ��x-3��2=1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
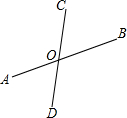 ��ͼ��ֱ��AB��CD�ཻ�ڵ�O������DOB�ǡ�COB��2�������AOC=��������
��ͼ��ֱ��AB��CD�ཻ�ڵ�O������DOB�ǡ�COB��2�������AOC=��������| A�� | 150�� | B�� | 120�� | C�� | 110�� | D�� | 100�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
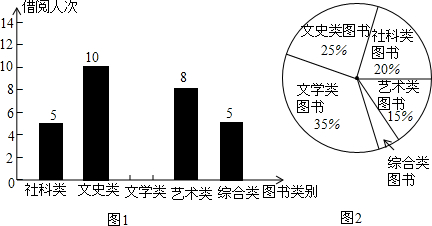
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com