
如图是某通道的侧面示意图,已知AB∥CD∥EF,AM∥BC∥DE,AB=CD=EF,∠BAM=30°,AB=6m.
(1)求FM的长;
(2)连接AF,若sin∠FAM=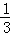 ,求AM的长.
,求AM的长.

科目:初中数学 来源: 题型:
某校规定:学生的数学学期 综合成绩是由平时、期中和期末三项成绩按3:3:4的比例计算所得.若某同学本学期数学的平时、期中和期末成绩分别是90分,90分和85分,则他本学期数学学期综合成绩是 分.
综合成绩是由平时、期中和期末三项成绩按3:3:4的比例计算所得.若某同学本学期数学的平时、期中和期末成绩分别是90分,90分和85分,则他本学期数学学期综合成绩是 分.
查看答案和解析>>
科目:初中数学 来源: 题型:
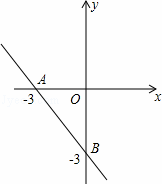
在平面直角坐标系中,一次函数y=kx+b的图象与x轴、y轴分别相交于A(﹣3,0),B(0,﹣3)两点,二次函数y=x2+mx+n的图象经过点A.
(1)求一次函数y=kx+b的解析式;
(2)若二次函数y=x2+mx+n图象的顶点在直线AB上,求m,n的值;
(3)当﹣3≤x≤0时,二次函数y=x2+mx+n的最小值为﹣4,求m,n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com