����⣺��1��������y=-x
2+2kx-
k
2+2k-2��k��ʵ������x���н��㣬
���б�ʽ��=��2k��
2+4��-
k
2+2k-2��=-��k-2��
2��0��
��k=2��
��������ߵĽ���ʽ�ǣ�y=-x
2+4x-4��
��������������ƽ��1����λ��������ƽ��4����λ�õ����������ǣ�y=-��x+1��
2+4��x+1��-4+4��
����y=-x
2+2x+3
��y=-��x-1��
2+4��
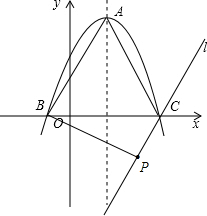
�ඥ��A����Ϊ��1��4����
��2����y=0����-x
2+2x+3=0����B��-1��0����C��3��0��
��ֱ��AB�ĺ�����ϵʽΪy=kx+b��
��A��0��4����B��-1��0����
���
��
��y=2x+2
��ֱ��l��AB�ҹ���C��3��0������ֱ��l�ĺ�����ϵʽΪy=2x-6��
�ߵ�P��l��һ�����Һ�����Ϊt�����P����Ϊ��t��2t-6��

��P��x���·�ʱ��t��3����S=S
��ABC+S
��BCP=
��4��4+
��4��|2t-6|=20-4t��
��0��S��16����0��20-4t��16����1��t��5����t��3����1��t��3
��P��x���Ϸ�ʱ��t��3����
��PM��x����M����Գ�����x�ύ��ΪN�� ��
S=S
����ANMP+S
��ANB+S
��PMC=
[4+��2t-6��]•��t-1��+
��2��4-
��t-3����2t-6��
=4t-4
��������ֱ��l��AB�����ݵȵȸߵ������Ƚ���ת��
S=S
��ABC+S
��APC=S
��ABC+S
��BPC=S
��ABC+S
��PBC=
��4��4+
��4����2t-6��=4t-4
��0��S��16����0��4t-4��16��
��1��t��5��
�֡�t��3��
��3��t��5��
��t��ȡֵ��Χ��1��t��3��3��t��5��
��3��AB=2
������C��CH��AB��HΪ���㣬S
��ABC=
��4��4=
��AB��CH
����CH=
��
��Ϊƽ������봦����ȣ����Ե�Q��ֱ��AB�ľ������
��
���Ե�R=
ʱ���У�R
��ʱ�ཻ��R��
ʱ���룮

 ����ƽ��1����λ��������ƽ��4����λ���õ��µ�������E����������E��x��Ľ���ΪB��C����ͼ��
����ƽ��1����λ��������ƽ��4����λ���õ��µ�������E����������E��x��Ľ���ΪB��C����ͼ��



 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
 ��1����b+c��ֵ��
��1����b+c��ֵ�� ��2012•�����һģ����ͼ����ƽ��ֱ������ϵxOy�У���֪������y=x2+bx+c����A��0��3����B��1��0�����㣬����ΪM��
��2012•�����һģ����ͼ����ƽ��ֱ������ϵxOy�У���֪������y=x2+bx+c����A��0��3����B��1��0�����㣬����ΪM��