
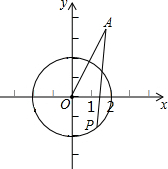 如图,在直角坐标中,⊙0的半径为2,圆心是原点,点A的坐标为(2,2$\sqrt{3}$),P是⊙0上的动点,连接AP,当∠OAP最大时,则点P坐标为(2,0)或(-1,$\sqrt{3}$).
如图,在直角坐标中,⊙0的半径为2,圆心是原点,点A的坐标为(2,2$\sqrt{3}$),P是⊙0上的动点,连接AP,当∠OAP最大时,则点P坐标为(2,0)或(-1,$\sqrt{3}$). 分析 由题意可知当∠OAP最大时,则AP和圆相切,由此即可求出满足题意的点P坐标.
解答 解:∵点A的坐标为(2,2$\sqrt{3}$),
∴AO=$\sqrt{{2}^{2}+(2\sqrt{3})^{2}}$=4,
由题意当∠OAP最大时,则AP和圆相切,过点A作圆的切线AP′,AP″,连接OP′,过P′作P′B⊥OP″,
∵点A的横坐标为2,OP″⊥AP″,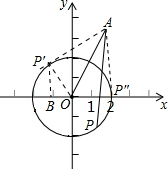
∴P″的坐标为(2,0);
∵AO=4,OP′=2,
∴∠P′AO=30°,
∴∠BP′O=30°,
∵P′O=2,
∴BO=1,
∴P′B=$\sqrt{3}$,
∴点P″的坐标为(-1,$\sqrt{3}$),
综上可知,点P的坐标为(2,0)或(-1,$\sqrt{3}$).
点评 本题考查了切线的性质、勾股定理的运用、特殊角的三角函数值,解题的关键是确定点P的位置,做到不重不漏.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
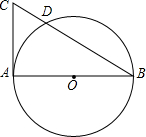 如图,AB为⊙O的直径,CA切⊙O于A,CB交⊙O于D,若CD=2,BD=6,求半径r=( )
如图,AB为⊙O的直径,CA切⊙O于A,CB交⊙O于D,若CD=2,BD=6,求半径r=( )| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | 4$\sqrt{3}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com