
【题目】如图,AB∥CD,OE平分∠BOC,OF⊥OE, OP⊥CD,∠ABO=40°,则下列结论:①∠BO E=70°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论有(填序号)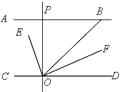
【答案】①②③
【解析】∵AB∥CD,
∴∠ABO=∠BOD=40°,
∴∠BOC=180°﹣40°=140°,
∵OE平分∠BOC,
∴∠BOE=70°;所以①正确;
∵OF⊥OE,
∴∠E OF=90°,
∴∠ BOF=90°﹣70°=20°,
∴∠BOF=∠BOD,所以②正确;
∵OP⊥CD,
∴∠COP=90°,
∴∠POE=90°﹣∠EOC=20°,
∴∠POE=∠BOF; 所以③正确;
∴∠POB=70°﹣∠POE=50°,
而∠DOF=20 °,所以④错误.
故答案为①②③.
根据二直线平行内错角相等得出∠ABO=∠BOD=40°,根据邻补角的定义得出∠BOC=180°﹣40°=140°,根据角平分线的性质得出∠BOE=70° ,根据垂直的定义及角的和差得出∠ BOF=90°﹣70°=20° ,进而得出∠BOF=∠BOD ,根据垂直的定义及角的和差得出∠POE=90°﹣∠EOC=20°,从而得出∠POE=∠BOF;进而得出∠POB=70°﹣∠POE=50°,而∠DOF=20 ° 故∠POB≠2∠DOF 。


科目:初中数学 来源: 题型:
【题目】如图反映的过程是:小强从家去菜地浇水,又去玉米地除草,然后回家.如果菜地和玉米地的距离为a千米,小强在玉米地除草比在菜地浇水多用的时间为b分钟,则a,b的值分别为( )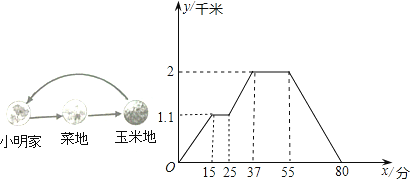
A.1.1,8
B.0.9,3
C.1.1,12
D.0.9,8
查看答案和解析>>
科目:初中数学 来源: 题型:
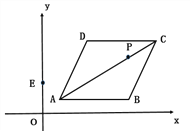
【题目】已知菱形ABCD在平面直角坐标系的位置如图所示,A(1,1),B(6,1),AC=4![]() ,点P是对角线AC上的一个动点,E(0,2),当
,点P是对角线AC上的一个动点,E(0,2),当![]() 周长最小时,点P的坐标为( ).
周长最小时,点P的坐标为( ).
A. (2,2) B. (2, ![]() ) C. (
) C. (![]() ,
, ![]() ) D. (
) D. (![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上点A表示的数为8,B是数轴上一点,且AB=14,动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.![]()
(1)(1)点B表示的数为 , 点P表示的数为(用含t的式子表示);
(2)动点H从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P,H同时出发,问点P运动多少秒时追上点H?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的个数有( )
①在同一平面内不相交的两条线段必平行;
②在同一平面内不相交的两条直线必平行;
③在同一平面内不平行的两条线段必相交;
④在同一平面内不平行的两条直线必相交.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从全校1200名学生中随机选取一部分学生进行调查,调查情况:A、上网时间≤1小时;B、1小时<上网时间≤4小时;C、4小时<上网时间≤7小时;D、上网时间>7小时.统计结果制成了如图统计图: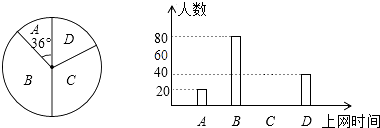
(1)参加调查的学生有人;
(2)请将条形统计图补全;
(3)请估计全校上网不超过7小时的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度。已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).![]()
(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com