
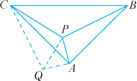
【题目】如图,在等腰直角三角形ABC中,∠BAC=90°,P是△ABC内一点,PA=1,PB=3,PC=![]() .求∠CPA的度数.
.求∠CPA的度数.
【答案】135°
【解析】由于△ABC为等腰直角三角形,AB=AC,则把△APB绕A点逆时针旋转90°可得到△AP′C,连PP′,根据旋转的性质得到∠P′AP=90°,P′A=PA=1,P′C=PB=3,得到△PAP′为等腰直角三角形,根据等腰直角三角形的性质得P′P=![]() PA=
PA=![]() ,∠APP′=45°,在△P′PC中,可得到PC2+P′P2=P′C2,根据勾股定理的逆定理得到△P′PC为直角三角形,∠CPP′=90°,利用∠CPA=∠CPP′+∠APP′进行计算即可.
,∠APP′=45°,在△P′PC中,可得到PC2+P′P2=P′C2,根据勾股定理的逆定理得到△P′PC为直角三角形,∠CPP′=90°,利用∠CPA=∠CPP′+∠APP′进行计算即可.
∵△ABC为等腰直角三角形,AB=AC,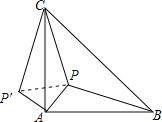
∴把△APB绕A点逆时针旋转90°可得到△AP′C,连PP′,如图,
∴∠P′AP=90°,P′A=PA=1,P′C=PB=3,
∴△PAP′为等腰直角三角形,
∴P′P=![]() PA=
PA=![]() ,∠APP′=45°,
,∠APP′=45°,
在△P′PC中,P′C=3,P′P=![]() ,PC=
,PC=![]() ,
,
∵(![]() )2+(
)2+(![]() )2=32,
)2=32,
∴PC2+P′P2=P′C2,
∴△P′PC为直角三角形,∠CPP′=90°,
∴∠CPA=∠CPP′+∠APP′=90°+45°=135°.
“点睛”本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了勾股定理的逆定理以及等腰直角三角形的判定与性质.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】电子跳蚤游戏盘是如图所示的△ABC,AB=6,AC=7,BC=8。如果跳蚤开始时在BC边的P0处,BP0=2。跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;……;跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2007与P2010之间的距离为( )。
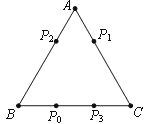
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度为 米.(结果保留根号)
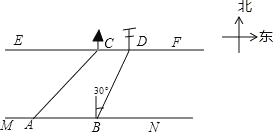
查看答案和解析>>
科目:初中数学 来源: 题型:
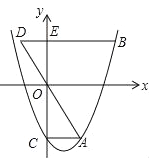
【题目】(2016浙江省温州市第23题)如图,抛物线y=x2﹣mx﹣3(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
(1)用含m的代数式表示BE的长.
(2)当m=![]() 时,判断点D是否落在抛物线上,并说明理由.
时,判断点D是否落在抛物线上,并说明理由.
(3)若AG∥y轴,交OB于点F,交BD于点G.
①若△DOE与△BGF的面积相等,求m的值.
②连结AE,交OB于点M,若△AMF与△BGF的面积相等,则m的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
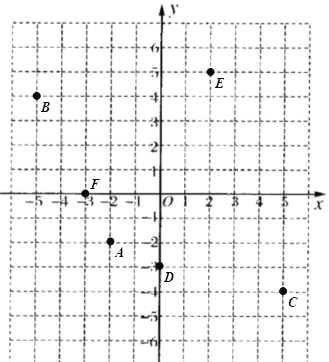
【题目】(1)写出图中点A、B、C、D、E、F的坐标.
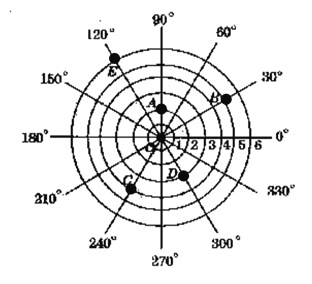
(2)如图是一台雷达探测相关目标得到的结果,若记图中目标A的位置为(2,90°),则其余各目标的位置分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
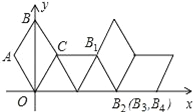
【题目】如图,在平面直角坐标系中有一菱形OABC且∠A=120°,点O、B在y轴上,OA=1,现在把菱形向右无滑动翻转,每次翻转60°,点B的落点依次为B1、B2、B3…,连续翻转2017次,则B2017的坐标为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com