
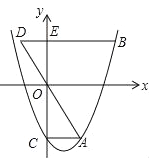
【题目】(2016浙江省温州市第23题)如图,抛物线y=x2﹣mx﹣3(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
(1)用含m的代数式表示BE的长.
(2)当m=![]() 时,判断点D是否落在抛物线上,并说明理由.
时,判断点D是否落在抛物线上,并说明理由.
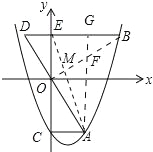
(3)若AG∥y轴,交OB于点F,交BD于点G.
①若△DOE与△BGF的面积相等,求m的值.
②连结AE,交OB于点M,若△AMF与△BGF的面积相等,则m的值是 .
【答案】(1)、2m;(2)、落在抛物线上;(3)、①、m=![]() ;②、m=
;②、m=![]()
【解析】
试题分析:(1)、根据A、C两点纵坐标相同,求出点A横坐标即可解决问题;(2)、求出点D坐标,然后判断即可;(3)、①首先根据EO=2FG,证明BG=2DE,列出方程即可解决问题;②求出直线AE、BO的解析式,求出交点M的横坐标,列出方程即可解决问题.
试题解析:(1)、∵C(0,﹣3),AC⊥OC, ∴点A纵坐标为-3, y=-3时 -3=x2﹣mx-3,解得x=0或m,
∴点A坐标(m,﹣3), ∴AC=m, ∴BE=2AC=2m.
(2)、∵m=![]() , ∴点A坐标(
, ∴点A坐标(![]() ,﹣3), ∴直线OA为y=﹣
,﹣3), ∴直线OA为y=﹣![]() x, ∴抛物线解析式为y=x2﹣
x, ∴抛物线解析式为y=x2﹣![]() x﹣3,
x﹣3,
∴点B坐标(2![]() ,3), ∴点D纵坐标为3, 对于函数y=﹣
,3), ∴点D纵坐标为3, 对于函数y=﹣![]() x,当y=3时,x=﹣
x,当y=3时,x=﹣![]() ,
,
∴点D坐标(﹣![]() ,3). ∵对于函数y=x2﹣
,3). ∵对于函数y=x2﹣![]() x﹣3,x=﹣
x﹣3,x=﹣![]() 时,y=3,
时,y=3,
∴点D在落在抛物线上.
(3)、①∵∠ACE=∠CEG=∠EGA=90°, ∴四边形ECAG是矩形, ∴EG=AC=BG, ∵FG∥OE,
∴OF=FB,∵EG=BG, ∴EO=2FG, ∵![]() DEEO=
DEEO=![]() GBGF, ∴BG=2DE, ∵DE∥AC, ∴
GBGF, ∴BG=2DE, ∵DE∥AC, ∴![]() =
=![]() =
=![]() ,
,
∵点B坐标(2m,2m2﹣3), ∴OC=2OE, ∴3=2(2m2﹣3), ∵m>0, ∴m=![]() .
.
②∵A(m,﹣3),B(2m,2m2﹣3),E(0,2m2﹣3),
∴直线AE解析式为y=﹣2mx+2m2﹣3,直线OB解析式为y=![]() x,
x,
由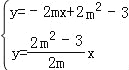 消去y得到﹣2mx+2m2﹣3=
消去y得到﹣2mx+2m2﹣3=![]() x,解得x=
x,解得x=![]() ,
,
∴点M横坐标为![]() , ∵△AMF的面积=△BFG的面积,
, ∵△AMF的面积=△BFG的面积,
∴![]() (
(![]() +3)(m﹣
+3)(m﹣![]() )=
)=![]() m
m![]() (2m2﹣3), 整理得到:2m4﹣9m2=0, ∵m>0,
(2m2﹣3), 整理得到:2m4﹣9m2=0, ∵m>0,
∴m=![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
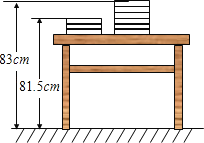
【题目】某班教室里,两摞七年级上册数学《补充习题》整齐地叠放在课桌上,请根据图中所给出的数据信息,解答下列问题:
(1)每本数学《补充习题》的厚度为___cm,课桌的高度为___cm;
(2)当一摞叠放在桌面上的数学《补充习题》的本数为x(本)时,请写出这一摞数学《补充习题》高出地面的距离为________________cm(用含x的代数式表示);
(3)若桌面上有60本数学《补充习题》整齐地叠放成一摞,小亮从中取走他们小组的16本,求余下的数学《补充习题》高出地面的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2向上平移2个单位,再向左平移3个单位得到的抛物线解析式为( )
A. y=﹣(x+3)2+2 B. y=﹣(x﹣3)2+2
C. y=﹣(x+3)2﹣2 D. y=﹣(x﹣3)2﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
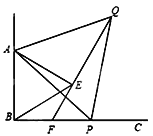
【题目】如图, 已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连接QE并延长交BP于点F. 试说明:(1)△ABP≌△AEQ;(2)EF=BF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com