
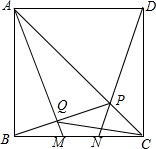
 如图,M,N是正方形ABCD的边BC上两个动点,满足BM=CN,连结AC交DN于点P,连结AM交BP于点Q,若正方形的边长为1,则线段CQ的最小值是$\frac{\sqrt{5}-1}{2}$.
如图,M,N是正方形ABCD的边BC上两个动点,满足BM=CN,连结AC交DN于点P,连结AM交BP于点Q,若正方形的边长为1,则线段CQ的最小值是$\frac{\sqrt{5}-1}{2}$. 分析 首先证明的Q在以AB为直径的圆上运动,连接OC与⊙O交于点Q′,此时CQ′最小,根据勾股定理即可计算.
解答 解: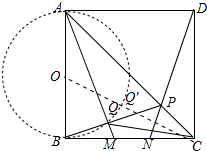 ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABC=∠BCD=∠CDA=∠DAB=90°,∠ACB=∠ACD=45°
在△ABM和△DCN中,
$\left\{\begin{array}{l}{AB=DC}\\{∠ABM=∠DCN}\\{BM=CN}\end{array}\right.$,
∴△ABM≌△DCN,
∴∠BAM=∠CDN,
在△CPB和△CPD中,
$\left\{\begin{array}{l}{CP=CP}\\{∠PCB=∠PCD}\\{CB=CD}\end{array}\right.$,
∴△CPD≌△CPB,
∴∠CDP=∠CBP=∠BAM,
∵∠CBP+∠ABP=90°,
∴∠BAM+∠ABP=90°,
∴∠AQB=90°,
∴点Q在以AB为直径的圆的圆上运动,设圆心为O,连接OC交⊙O于点Q′,此时CQ′最小,
∴CQ′=OC-OQ′=$\sqrt{{1}^{2}+(\frac{1}{2})^{2}}$-$\frac{1}{2}$=$\frac{\sqrt{5}-1}{2}$.
故答案为$\frac{\sqrt{5}-1}{2}$.
点评 本题考查正方形的性质、圆、勾股定理等知识,解题的关键是证明点Q在以AB为直径的圆上运动,找到点Q的位置,题目比较难,属于中考填空题中的压轴题.


 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:解答题
 如图,已知△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E.
如图,已知△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
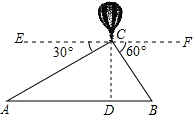 如图所示,从热气球C上测定建筑物A、B底部的俯角分别为30°和60°,已知AB间的距离为180米,CD垂直于AB于点D.问:此时热气球的高度为多少?
如图所示,从热气球C上测定建筑物A、B底部的俯角分别为30°和60°,已知AB间的距离为180米,CD垂直于AB于点D.问:此时热气球的高度为多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
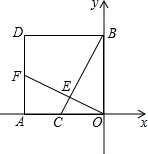 如图,边长为4的正方形OADB的边OA、OB分别在x轴、y轴上,点C为OA的中点,OF⊥BC于E,交AD于F.
如图,边长为4的正方形OADB的边OA、OB分别在x轴、y轴上,点C为OA的中点,OF⊥BC于E,交AD于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com