
分析 (1)分别计算出两个不等式的解集,再根据大小小大中间找确定不等式组的解集;
(2)分别计算出两个不等式的解集,再根据大大小小找不到确定不等式组的解集.
解答 解:(1)$\left\{\begin{array}{l}{3x+6≤15①}\\{-2x+4≤6②}\end{array}\right.$,
由①得:x≤3,
由②得:x≥-1,
不等式组的解集为-1≤x≤3,
在数轴上表示为: ;
;
(2)$\left\{\begin{array}{l}{x-2(x-2)<-1①}\\{2(x+2)-(1+x)≤1②}\end{array}\right.$,
由①得:x>5,
由②得:x≤-2,
不等式组的解集为:无解,
在数轴上表示为: .
.
点评 此题主要考查了一元一次不等式组的解法,以及在数轴上表示不等式组的解集,关键是掌握解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.


科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
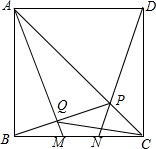 如图,M,N是正方形ABCD的边BC上两个动点,满足BM=CN,连结AC交DN于点P,连结AM交BP于点Q,若正方形的边长为1,则线段CQ的最小值是$\frac{\sqrt{5}-1}{2}$.
如图,M,N是正方形ABCD的边BC上两个动点,满足BM=CN,连结AC交DN于点P,连结AM交BP于点Q,若正方形的边长为1,则线段CQ的最小值是$\frac{\sqrt{5}-1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
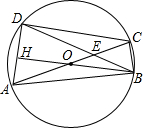 如图,四边形ABCD内接于⊙O,对角线AC经过圆心O.且交BD于点E,BO⊥AD于点H,OA=AD=2,则OE:EC值是( )
如图,四边形ABCD内接于⊙O,对角线AC经过圆心O.且交BD于点E,BO⊥AD于点H,OA=AD=2,则OE:EC值是( )| A. | 1:2 | B. | 1:$\sqrt{2}$ | C. | 1:$\sqrt{3}$ | D. | $\sqrt{2}$:$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | ②④①③ | B. | ③①④② | C. | ②④③① | D. | ①③②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com