
【题目】如图,在△ABC中,AB=AC=1,BC= ![]() ,在AC边上截取AD=BC,连接BD.
,在AC边上截取AD=BC,连接BD.
(1)通过计算,判断AD2与ACCD的大小关系;
(2)求∠ABD的度数.
【答案】
(1)
解:∵AB=BC=1,BC= ![]() ,
,
∴AD= ![]() ,DC=1﹣
,DC=1﹣ ![]() =
= ![]() .
.
∴AD2= ![]() =
= ![]() ,ACCD=1×
,ACCD=1× ![]() =
= ![]() .
.
∴AD2=ACCD
(2)
解:∵AD=BD,AD2=ACCD,
∴BD2=ACCD,即 ![]() .
.
又∵∠C=∠C,
∴△BCD∽△ABC.
∴ ![]() ,∠DBC=∠A.
,∠DBC=∠A.
∴DB=CB=AD.
∴∠A=∠ABD,∠C=∠D.
设∠A=x,则∠ABD=x,∠DBC=x,∠C=2x.
∵∠A+∠ABC+∠C=180°,
∴x+2x+2x=180°.
解得:x=36°.
∴∠ABD=36°
【解析】(1)先求得AD、CD的长,然后再计算出AD2与ACCD的值,从而可得到AD2与ACCD的关系;(2)由(1)可得到BD2=ACCD,然后依据对应边成比例且夹角相等的两三角形相似证明△BCD∽△ABC,依据相似三角形的性质可知∠DBC=∠A,DB=CB,然后结合等腰三角形的性质和三角形的内角和定理可求得∠ABD的度数.本题主要考查的是相似三角形的性质和判定、等腰三角形的性质、三角形内角和定理的应用,证得△BCD∽△ABC是解题的关键.
【考点精析】解答此题的关键在于理解相似三角形的判定的相关知识,掌握相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在甲、乙两名同学中选拔一人参加“中华好诗词”大赛,在相同的测试条件下,两人5次测试成绩(单位:分)如下:
甲:79,86,82,85,83
乙:88,79,90,81,72.
回答下列问题:
(1)甲成绩的平均数是 , 乙成绩的平均数是;
(2)经计算知S甲2=6,S乙2=42.你认为选拔谁参加比赛更合适,说明理由;
(3)如果从甲、乙两人5次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于80分的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:
①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的是( )
A.②④⑤⑥
B.①③⑤⑥
C.②③④⑥
D.①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是 ![]() 上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
A.(sinα,sinα)
B.(cosα,cosα)
C.(cosα,sinα)
D.(sinα,cosα)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1的解析表达式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2,交于点C.
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更好的治理水质,保护环境,市治污办事处预购买10台污水处理设备,现有A、B两种型号的设备,其中价格及污水处理量如下表:
A型 | B型 | |
价格(万元) | a | b |
处理污水量(吨/月) | 240 | 200 |
询问商家得知:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元,根据以上条件.
(1)求a、b的值;
(2)市污水处理办公室由于资金缺乏,购买污水处理设备的资金最多105万元,你认为该有几种购买方案?
(3)在(2)的情况下,若每月污水处理量要求不低于2040吨,为节约资金,请你帮污水处理办事处选取一种最省钱的方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=x2+(k﹣1)x﹣k与直线y=kx+1交于A,B两点,点A在点B的左侧.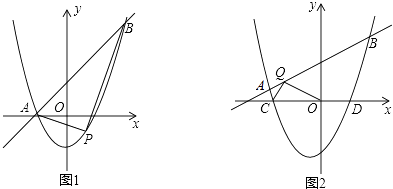
(1)如图1,当k=1时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线y=x2+(k﹣1)x﹣k(k>0)与x轴交于点C、D两点(点C在点D的左侧),在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD等于海里.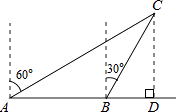
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解学校开展“孝敬父母,从家务劳动做起”活动的实施情况,该校抽取八年级![]() 名学生,调查他们一周(按七天计算)做家务所用时间(单位:小时)得到一组数据,绘制成下表:
名学生,调查他们一周(按七天计算)做家务所用时间(单位:小时)得到一组数据,绘制成下表:
时间 | 划记 | 人数 | 所占百分比 |
|
|
|
|
| 正正正 |
|
|
| 正正 |
| |
| 正 |
|
|
| 正 |
|
|
| 正 |
| |
| 正 |
| |
合计 |
|
|
(1)请填表中未完成的部分;
(2)根据以上信息判断,每周做家务的时间不超过![]() 小时的学生所占的百分比是多少?
小时的学生所占的百分比是多少?
(3)针对以上情况,写出一个20字以内的倡导“孝敬父母,热爱劳动”的句子.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com