
分析 首先将无理方程整理为整式方程,进而利用因式分解法分解因式,再利用换元法求出x的值,进而检验得出.
解答 解:把$\sqrt{x-\frac{1}{x}}$移到等号的左边,然后两边平方的得到:x2+x-$\frac{1}{x}$-2x$\sqrt{x-\frac{1}{x}}$=1-$\frac{1}{x}$,
整理得:x2+x-1=2x$\sqrt{x-\frac{1}{x}}$,
再平方,得:x4+x2+1-2x+2x3-2x2=4x3-4x;
整理得:x4-2x3-x2+2x+1=0
则(x-1)x(x+1)(x-2)=-1.
分组展开,前两项一组,后两项一组,展开后得 (x2-x)(x2-x-2)=-1
令 a=x2-x
则原方程化为 a(a-2)=-1
即 a2-2a+1=0
a1=a2=1
所以 x2-x=1
解得 x1=$\frac{1+\sqrt{5}}{2}$,x2=$\frac{1-\sqrt{5}}{2}$,
将x2带回原方程$\sqrt{1-\frac{1}{x}}$=x-$\sqrt{x-\frac{1}{x}}$,发现x-$\sqrt{x-\frac{1}{x}}$<0,方程不成立,
而x1=$\frac{1+\sqrt{5}}{2}$能使原方程成立,
所以原方程的解为:x=$\frac{1+\sqrt{5}}{2}$.
点评 此题主要考查了无理方程的解法,正确转化方程形式是解题关键.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4、6、8 | B. | $\sqrt{3}$、$\sqrt{4}$、$\sqrt{5}$ | C. | 32、42、52 | D. | 2$\sqrt{3}$、4$\sqrt{2}$、2$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
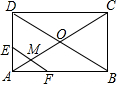 如图,在矩形ABCD中,对角线AC与BD相交于点O,点M为线段AC上一个动点,过点M作EF∥BD交AD(或DC)于点E,交AB(或BC)于点F,设AM=x,EF=y,则y关于x的函数图象大致形状是( )
如图,在矩形ABCD中,对角线AC与BD相交于点O,点M为线段AC上一个动点,过点M作EF∥BD交AD(或DC)于点E,交AB(或BC)于点F,设AM=x,EF=y,则y关于x的函数图象大致形状是( )| A. | 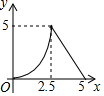 | B. | 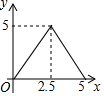 | C. | 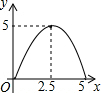 | D. | 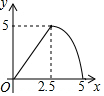 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com