
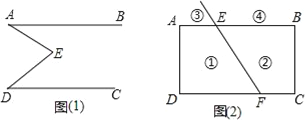
【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)
【答案】(1)①∠AED=70°;
②∠AED=80°;
③猜想:∠AED=∠EAB+∠EDC,证明见解析;
(2)点P在区域①时,∠EPF=360°﹣(∠PEB+∠PFC);
点P在区域②时,∠EPF=∠PEB+∠PFC;
点P在区域③时,∠EPF=∠PEB﹣∠PFC;
点P在区域④时,∠EPF=∠PFC﹣∠PEB.
【解析】(1)①根据图形猜想得出所求角度数即可;
②根据图形猜想得出所求角度数即可;
③猜想得到三角关系,理由为:延长AE与DC交于F点,由AB与DC平行,利用两直线平行内错角相等得到一对角相等,再利用外角性质及等量代换即可得证;
(2)分四个区域分别找出三个角关系即可.
解:(1)①∠AED=70°;
②∠AED=80°;
③猜想:∠AED=∠EAB+∠EDC,
证明:延长AE交DC于点F,
∵AB∥DC,
∴∠EAB=∠EFD,
∵∠AED为△EDF的外角,
∴∠AED=∠EDF+∠EFD=∠EAB+∠EDC;
(2)根据题意得:
点P在区域①时,∠EPF=360°﹣(∠PEB+∠PFC);
点P在区域②时,∠EPF=∠PEB+∠PFC;
点P在区域③时,∠EPF=∠PEB﹣∠PFC;
点P在区域④时,∠EPF=∠PFC﹣∠PEB.
“点睛”此题考查了平行线的性质,熟练掌握平行线的性质是解本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两台机器共加工一批零件,在加工过程中两台机器均改变了一次工作效率.从工作开始到加工完这批零件两台机器恰好同时工作6小时.甲、乙两台机器各自加工的零件个数y(个)与加工时间x(时)之间的函数图象分别为折线OA﹣AB与折线OC﹣CD.如图所示.
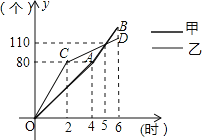
(1)甲机器改变工作效率前每小时加工零件 个.
(2)求乙机器改变工作效率后y与x之间的函数关系式,并求出自变量x的取值范围.
(3)求这批零件的总个数.
(4)直接写出当甲、乙两台机器所加工零件数相差10个时,x的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
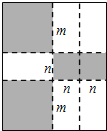
如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为m厘米的大正方形,两块是边长都为n厘米的小正方形,五块是长宽分别是m厘米、n厘米的全等小矩形,且m>n.
(1)用含m、n的代数式表示切痕的总长为_____________厘米;
(2)若每块小矩形的面积为48厘米2,四个正方形的面积和为200厘米2,试求(m+n)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
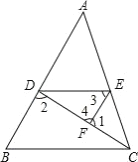
填空:
如图,已知∠1+∠2=180°,∠3=∠B,求证:∠AED=∠ACB.
证明:∵∠1+∠2=180°(已知)
∠1+________=180°(邻补角的定义)
∴∠2=________(同角的补角定义)
∴AB∥EF(___________________)
∴∠3=________(_____________________)
又∵∠3=∠B(已知)
∴∠B=________(等量代换)
∴DE∥BC(_________________)
∴∠AED=∠ACB(__________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.
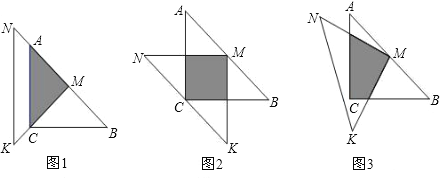
(1)如图1,两个三角尺的重叠部分为△ACM,则重叠部分的面积为 ,周长为 .
(2)将图1中的△MNK绕顶点M逆时针旋转45°,得到图2,此时重叠部分的面积为 ,周长为 .
2(3)如果将△MNK绕M旋转到不同于图1,图2的位置,如图3所示,猜想此时重叠部分的面积为多少?并试着加以验证.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 (2016湖南湘西州第14题)一个等腰三角形一边长为4cm,另一边长为5cm,那么这个等腰三角形的周长是( )
A.13cm B.14cm C.13cm或14cm D.以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次数学知识竞赛共有30道题,规定,答对一道题得4分,不答或答错一道题倒扣2分,若甲同学答对25题,答错5道题,则甲 同学得________分,若得分低于60分者获奖,则获奖者至少应答对________道题。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com