
����Ŀ���ס�����̨�������ӹ�һ��������ڼӹ���������̨�������ı���һ�ι���Ч�ʣ��ӹ�����ʼ���ӹ������������̨����ǡ��ͬʱ����6Сʱ���ס�����̨�������Լӹ����������y��������ӹ�ʱ��x��ʱ��֮��ĺ���ͼ��ֱ�Ϊ����OA��AB������OC��CD����ͼ��ʾ��
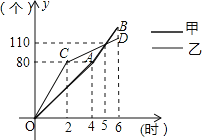
��1�������ı乤��Ч��ǰÿСʱ�ӹ���� ����
��2�����һ����ı乤��Ч�ʺ�y��x֮��ĺ�����ϵʽ��������Ա���x��ȡֵ��Χ��
��3��������������ܸ�����
��4��ֱ��д�����ס�����̨�������ӹ���������10��ʱ��x��ֵΪ ��
���𰸡���1��20����2��y��=10x+60��2��x��6������3��260����4��![]() ��
��
���������⣺��1��80��4=20��������
�ʴ�Ϊ��20��
��2����ͼ���C��2��80����D��5��110����
�������ʽΪy=kx+b��k��0����
��![]() ����ã�
����ã�![]() ��
��
��y��=10x+60��2��x��6����
��3����AB����4��80������5��110����
����AB�Ľ���ʽΪy��=mx+n��m��0����
��![]() ����ã�
����ã�![]() ��
��
��y��=30x��40��4��x��6����
��x=6ʱ��y��=30��6��40=140��y��=10��6+60=120��
������������ܸ�����140+120=260��
��4��40x��10=20x��
��ã�x=![]() ��
��
10x+60��10=30x��40��
��ã�x=![]() ��
��
30x��40��10=10x+60��
��ã�x=![]() ��
��
���ס�����̨�������ӹ���������10��ʱ��x��ֵΪ![]() ��
��
�ʴ�Ϊ��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˴����������ij��У�ʵ�ֿ�Խʽ��չ������������������Ͷ�ʼƻ������ƽ����������蹤�̲������·������Ҫ������ʯ�����ƻ�ÿСʱ�ھ���ʯ��540m3���־�����ij���ͻ�е����˾���üס��������ͺŵ��ھ������������������˾�ṩ���ھ���й���Ϣ�����

��1�������üס��������ͺŵ��ھ����8̨��ǡ�����ÿСʱ���ھ�������ס��������ͺŵ��ھ���������̨��
��2�����ÿСʱ֧���������850Ԫ����ǡ�����ÿСʱ���ھ�������ô���м��ֲ�ͬ�����÷�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ʽ�������ǣ� ��
A��83.5��=83��50��
B��37��12��36��=37.48��
C��24��24��24��=24.44��
D��41.25��=41��15��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������庣���ϣ�һ�ҽ�ž������ڻ���A�����������Ҿ�A��60�����B��ѵ����ͻȻ�ӵ��������Ҫ�ý�ǰ��C��������һ����Σ��������ҽԺ���Σ���֪C����A�ı�ƫ��30�㷽������B�ı�ƫ��60�㷽������B��������ƽ��ÿСʱ��ʻ30�����Ҫ����ʱ����ܰѻ��������͵�����ҽԺ������ȷ��0.1Сʱ��![]() ��1.7��
��1.7��
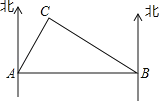
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������P��ƽ��ֱ������ϵ�а�ͼ�м�ͷ��ʾ�����˶�����1�δ�ԭ���˶����㣨1��1������2�ν����˶����㣨2��0������3�ν����˶����㣨3��2�����������������˶����ɣ�������2017���˶�����P��������______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и����߶�Ϊ�ߣ�������������ε���( )
A. 2cm��3cm��4cm B. 1cm��2cm��3cm
C. 3cm��4cm��5cm D. 4cm��2cm��3cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��x��4�����B��3��y������y��Գƣ���ôx+y��ֵΪ____________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ABCD�У�AB��CD��AD��AB����B=60����AB=10��BC=4����P���߶�AB�ӵ�A���B�˶�����AP=x��
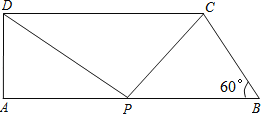
��1����AD�ij���
��2����P���˶������У��Ƿ������A��P��DΪ���������������P��C��BΪ��������������ƣ������ڣ����x��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
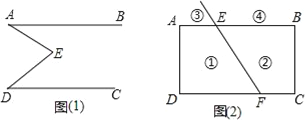
����Ŀ����ͼ��1����E��ֱ��AB��CD�ڲ�һ�㣬AB��CD������EA��ED��
��1��̽����
������A=30�㣬��D=40�㣬���AED���ڶ��ٶȣ�
������A=20�㣬��D=60�㣬���AED���ڶ��ٶȣ�
����ͼ��1���С�AED����EAB����EDC��ʲô������ϵ����֤����Ľ��ۣ�
��2����չ����ͼ��2��������FE�����ABCD�ı�AB���ڵ�E�����CD���ڵ�F���٢ڢֱܷۢ��DZ�����FE�������ĸ��������߽磬���Тۢ�λ��ֱ��AB���Ϸ�����P��λ�������ĸ������ϵ㣬���룺��PEB����PFC����EPF֮��Ĺ�ϵ������Ҫ��֤����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com