
【题目】已知正六边形的边心距为![]() ,求正六边形的中心角、边长、周长和面积.
,求正六边形的中心角、边长、周长和面积.
【答案】六边形的中心角为60°,边长为2,周长为12,面积为6![]() .
.
【解析】
试题首先根据题意作出图形,然后可得△OBC是等边三角形,然后由三角函数的性质,求得OB的长,继而求得正六边形的中心角、边长、周长和面积.
试题解析:如图,连接OB、OC,过点O作OH⊥BC于点H,
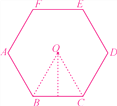
∵六边形ABCDEF是正六边形,∴∠BOC=![]() ×360°=60°.
×360°=60°.
∵OB=OC,∴△OBC是等边三角形.
∴∠OBC=60°,BC=OB=OC.
∵OH=![]() ,sin∠OBC=
,sin∠OBC=![]() ,
,
∴OB=BC=2.
∴正六边形的周长为2×6=12.
∴S正六边形ABCDEF=6S△OBC=6×![]() ×2×
×2×![]()
![]() =6
=6![]() .
.
∴正六边形的中心角为60°,边长为2,周长为12,面积为6![]() .
.


科目:初中数学 来源: 题型:
【题目】“C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)
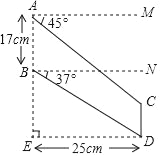
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PA,PB,AB,已知∠PBA=∠C.

(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB∶S四边形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC,其中正确结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
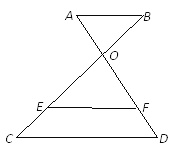
【题目】如图,已知AB∥EF∥CD,AD与BC相交于点O.
(1)如果CE=3,EB=9,DF=2,求AD的长;
(2)如果BO:OE:EC=2:4:3,AB=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c–3b<0;⑤a+b>n(an+b)(n≠1),其中正确的结论有( )
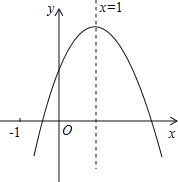
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
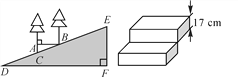
【题目】施工队准备在一段斜坡上铺上台阶方便通行.现测得斜坡上铅垂的两棵树间的水平距离AB=4 m,斜面距离BC=4.25 m,斜坡总长DE=85 m.
(1)求坡角∠D的度数(结果精确到1°);
(2)若这段斜坡用厚度为17 cm的长方体台阶来铺,需要铺几级台阶?(参考数据:cos20°≈0.94,sin20°≈0.34,sin18°≈0.31,cos18°≈0.95)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周长相等的正三角形、正四边形、正六边形的面积S3、S4、S6间的大小关系是( )
A. S3>S4>S6 B. S6>S4>S3 C. S6>S3>S4 D. S4>S6>S3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我区某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个足球和篮球为关注儿童戍长的健康,实施“关注肥胖守儿童计划”,某校结全校各班肥胖儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅不完整的统计图:
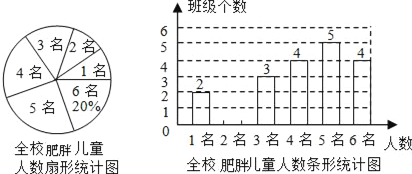
(1)全校班级个数 个 ,并将该条形统计图补充完整;
(2)为了了解肥胖儿重的饮食情况,某校决定从只有2名留守儿童的这些班级中,任选两名进行调查,请用列表法或画树形图的方法,求出所选两名肥胖儿童来自同一个班级的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com