
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c–3b<0;⑤a+b>n(an+b)(n≠1),其中正确的结论有( )
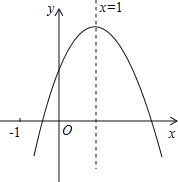
A. 2个 B. 3个 C. 4个 D. 5个
【答案】B
【解析】
①观察图象可知a<0,b>0,c>0,由此即可判定①;②当x=﹣1时,y=a﹣b+c由此可判定②;③由对称知,当x=2时,函数值大于0,即y=4a+2b+c>0,由此可判定③;④当x=3时函数值小于0,即y=9a+3b+c<0,且x=﹣![]() =1,可得a=﹣
=1,可得a=﹣![]() ,代入y=9a+3b+c<0即可判定④;⑤当x=1时,y的值最大.此时,y=a+b+c,当x=n时,y=an2+bn+c,由此即可判定⑤.
,代入y=9a+3b+c<0即可判定④;⑤当x=1时,y的值最大.此时,y=a+b+c,当x=n时,y=an2+bn+c,由此即可判定⑤.
①由图象可知:a<0,b>0,c>0,abc<0,故此选项错误;
②当x=﹣1时,y=a﹣b+c<0,即b>a+c,故此选项错误;
③由对称知,当x=2时,函数值大于0,即y=4a+2b+c>0,故此选项正确;
④当x=3时函数值小于0,y=9a+3b+c<0,且x=﹣![]() =1即a=﹣
=1即a=﹣![]() ,代入得9(﹣
,代入得9(﹣![]() )+3b+c<0,得2c<3b,故此选项正确;
)+3b+c<0,得2c<3b,故此选项正确;
⑤当x=1时,y的值最大.此时,y=a+b+c,而当x=n时,y=an2+bn+c,所以a+b+c>an2+bn+c,故a+b>an2+bn,即a+b>n(an+b),故此选项正确.
∴③④⑤正确.
故选B.


科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,E,F分别在边AC、BC上,满足AE=CF,连接BE,AF交于点P.
(1)求证:△ABE≌△CAF;
(2)求∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏的爸爸买了某项体育比赛的一张门票,她和哥哥两人都很想去观看.可门票只有一张,读九年级的哥哥想了一个办法,拿了8张扑克牌,将数字为2,3,5,9的四张牌给小敏,将数字为4,6,7,8的四张牌留给自己,并按如下游戏规则进行:小敏和哥哥从各自的四张牌中随机抽出一张,然后将两人抽出的两张扑克牌数字相加,如果和为偶数,则小敏去;如果和为奇数,则哥哥去.
【1】请用画树形图或列表的方法求小敏去看比赛的概率;
【2】哥哥设计的游戏规则公平吗?若公平,请说明理由;若不公平,请你设计一种公平的游戏规则.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,如果由甲队单独做这项工程刚好如期完成,若乙队单独做这项工程,要比规定日期多5天完成.现由若甲、乙两队合作4天后,余下的工程由乙队单独做,也正好如期完成.已知甲、乙两队施工一天的工程费分别为16万元和14万元.
(1)求规定如期完成的天数.
(2)现有两种施工方案:方案一:由甲队单独完成;方案二:先由甲、乙合作4天,再由乙队完成其余部分;通过计算说明,哪一种方案比较合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下内容,再解决问题.
在把多项式m2﹣4mn﹣12n2进行因式分解时,虽然它不符合完全平方公式,但是经过变形,可以利用完全平方公式进行分解:
m2﹣4mn﹣12n2=m2﹣4mn+4n2﹣4n2﹣12n2=(m﹣2n)2﹣16n2=(m﹣6n)(m+2n),像这样构造完全平方式的方法我们称之为“配方法”,利用这种方法解决下面问题.
(1)把多项式因式分解:a2﹣6ab+5b2;
(2)已知a、b、c为△ABC的三条边长,且满足4a2﹣4ab+2b2+3c2﹣4b﹣12c+16=0,试判断△ABC的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2011年5月20日是第22个中国学生营养日,某校社会实践小组在这天开展活动,调查快餐营养情况.他们从食品安全监督部门获取了一份快餐的信息(如图).根据信息,解答下列问题.
(1)求这份快餐中所含脂肪质量;
(2)若碳水化合物占快餐总质量的40%,求这份快餐所含蛋白质的质量;
(3)若这份快餐中蛋白质和碳水化合物所占百分比的和不高于85%,求其中所含碳水化合物质量的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
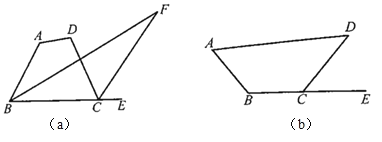
【题目】如图所示,在四边形![]() 中,
中,![]() 的角平分线及外角
的角平分线及外角![]() 的平分线所在的直线相交于点
的平分线所在的直线相交于点![]() ,若
,若![]() ,
,![]() .
.
(1)如图(a)所示,![]() ,试用
,试用![]() ,
,![]() 表示
表示![]() ,直接写出结论.
,直接写出结论.
(2)如图(b)所示,![]() ,请在图中画出
,请在图中画出![]() ,并试用
,并试用![]() ,
,![]() 表示
表示![]() .
.
(3)一定存在![]() 吗?若有,写出
吗?若有,写出![]() 的值;若不一定,直接写出
的值;若不一定,直接写出![]() ,
,![]() 满足什么条件时,不存在
满足什么条件时,不存在![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com