练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

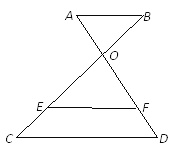
    【题目】如图，已知AB∥EF∥CD，AD与BC相交于点O.

    （1）如果CE=3，EB=9，DF=2，求AD的长；

    （2）如果BO：OE：EC=2：4：3，AB=3，求CD的长．

    【答案】（1）8；（2）

    【解析】

    试题（1）根据平行线分线段成比例、比例的基本性质求得AF=6，则AD=AF+FD=8；

    （2）由BO：OE：EC=2：4：3，可得BO：CO=2：7，根据AB∥CD得△ABO∽△DCO，则可得出AB:CD=BO:CO，求出CD的值.

    解：（1）∵AB∥EF∥CD，∴=，

    又∵CE=3，EB=9，DF=2，∴=，得AF=6,

    ∴AD=AF+FD=8.

    （2）∵BO：OE：EC=2：4：3，∴BO：CO=2：7，

    ∵AB∥CD，∴△ABO∽△DCO，

    ∴==，又AB=3，

    ∴CD=.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】把三角形按如图所示的规律拼图案，其中第①个图案中有4个三角形，第②个图案中有6个三角形，第③个图案中有8个三角形，…，按此规律排列下去，则第⑦个图案中三角形的个数为（ ）

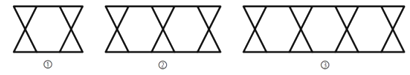
    A. 12 B. 14 C. 16 D. 18

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD内接于⊙O，点E在对角线AC上，EC=BC=DC

    （1）若∠CBD=39°，求∠BAD的度数

    （2）求证：∠1=∠2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（题文）识图理解：

    请认真观察如图给出的未来一周某市的每天的最高气温和最低气温，直接回答后面提出的问题：

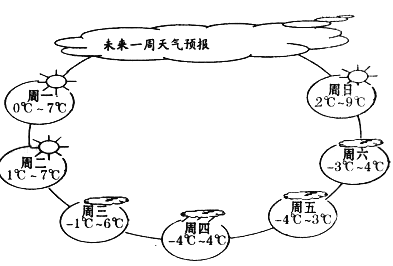
    （1）这一周该市的最高气温和最低气温分别是多少?

    （2）这一周中，星期几的温差最大?是多少?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠ACB=90°，D为AB上一点，以CD为直径的⊙O交BC于点E，连接AE交CD于点P，交⊙O于点F，连接DF，∠CAE=∠ADF．

    （1）判断AB与⊙O的位置关系，并说明理由；

    （2）若PF：PC=1：2，AF=5，求CP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知正六边形的边心距为，求正六边形的中心角、边长、周长和面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解：

    材料1．若一元二次方程ax2+bx+c=0(a≠0)的两根为x1，x2，则x1+x2=-，x1x2=．

    材料2．已知实数m，n满足m2-m-1=0，n2-n-1=0，且m≠n，求的值．

    解：由题知m，n是方程x2-x-1=0的两个不相等的实数根，

    根据材料1得m+n=1，mn=-1，

    ∴．

    解决问题：

    (1)一元二次方程x2-4x-3=0的两根为x1，x2，则x1+x2= ，x1x2= ．

    (2)已知实数m，n满足2m2-2m-1=0，2n2-2n-1=0，且m≠n，求m2n+mn2的值．

    (3)已知实数p，q满足p2=3p+2，2q2=3q+1，且p≠2q，求p2+4q2 的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

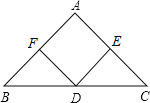
    【题目】如图，在△ABC中，点D是边BC的中点，DE⊥AC、DF⊥AB，垂足分别是E、F，且BF=CE．

    （1）求证：DE=DF；

    （2）当∠A=90°时，试判断四边形AFDE是怎样的四边形，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，弦AD，BC相交于点P，AD=BC．

    （1）求证：△ACB≌△BDA；

    （2）若∠ABC=35，则∠CAP= ．

    查看答案和解析>>

    同步练习册答案