
【题目】阅读理解:
材料1.若一元二次方程ax2+bx+c=0(a≠0)的两根为x1,x2,则x1+x2=-![]() ,x1x2=
,x1x2=![]() .
.
材料2.已知实数m,n满足m2-m-1=0,n2-n-1=0,且m≠n,求![]() 的值.
的值.
解:由题知m,n是方程x2-x-1=0的两个不相等的实数根,
根据材料1得m+n=1,mn=-1,
∴![]() .
.
解决问题:
(1)一元二次方程x2-4x-3=0的两根为x1,x2,则x1+x2= ,x1x2= .
(2)已知实数m,n满足2m2-2m-1=0,2n2-2n-1=0,且m≠n,求m2n+mn2的值.
(3)已知实数p,q满足p2=3p+2,2q2=3q+1,且p≠2q,求p2+4q2 的值.
【答案】(1)4,-3;(2)![]() ;(3)
;(3)![]()
【解析】
(1)直接根据根与系数的关系求解;
(2)利用m、n满足的等式,可把m、n可看作方程2x2-2x-1=0的两实数解,则根据根与系数的关系得到m+n=1,mn=-![]() ,接着把m2n+mn2分解得到mn(m+n),然后利用整体代入的方法计算;
,接着把m2n+mn2分解得到mn(m+n),然后利用整体代入的方法计算;
(3)先设t=2q,代入2q2=3q+1化简得到t2=3t+2,根据p与t满足的等式可把p与t(即2q)为方程x2-3x-2=0的两实数解,则根据根与系数的关系得到p+2q=3,p2q=-2,接着利用完全平方公式变形得到p2+4q2=(p+2q)2-2p2q,然后利用整体代入的方法计算.
(1)x1+x2=﹣![]() ,x1x2=﹣
,x1x2=﹣![]() ;
;
故答案为﹣![]() ,﹣
,﹣![]() ;
;
(2)∵m、n满足2m2﹣2m﹣1=0,2n2﹣2n﹣1=0,
∴m、n可看作方程2x2﹣2x﹣1=0的两实数解,
∴m+n=1,mn=﹣![]() ,
,
∴m2n+mn2=mn(m+n)=﹣![]() ×1=﹣
×1=﹣![]() ;
;
(3)设t=2q,代入2q2=3q+1化简为t2=3t+2,
则p与t(即2q)为方程x2﹣3x﹣2=0的两实数解,
∴p+2q=3,p2q=﹣2,
∴p2+4q2=(p+2q)2﹣2p2q=32﹣2×(﹣2)=13.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′,若∠CC′B′=33°,则∠B的大小是( )
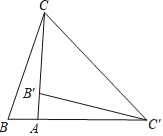
A. 33° B. 45° C. 57° D. 78°
查看答案和解析>>
科目:初中数学 来源: 题型:
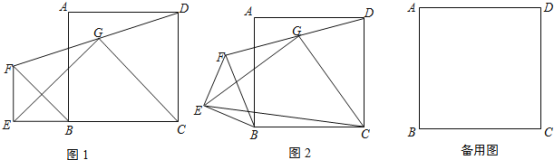
【题目】四边形ABCD是正方形,△BEF是等腰直角三角形,∠BEF=90°,BE=EF,连接DF,G为DF的中点,连接EG,CG,EC.
(1)如图1,若点E在CB边的延长线上,直接写出EG与GC的位置关系及![]() 的值;
的值;
(2)将图1中的△BEF绕点B顺时针旋转至图2所示位置,请问(1)中所得的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;
(3)将图1中的△BEF绕点B顺时针旋转α(0°<α<90°),若BE=1,![]() ,当E,F,D三点共线时,求DF的长及tan∠ABF的值.
,当E,F,D三点共线时,求DF的长及tan∠ABF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
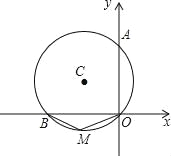
【题目】如图,⊙C 经过原点且与两坐标轴分别交于点 A 与点 B,点 B 的坐标为(﹣![]() ,0),M 是圆上一点,∠BMO=120°.⊙C 圆心 C 的坐标是_____.
,0),M 是圆上一点,∠BMO=120°.⊙C 圆心 C 的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】淇淇和嘉嘉在学习了利用相似三角形测高之后分别测量两个旗杆高度.
(1)如图1所示,淇淇将镜子放在地面上,然后后退直到她站直身子刚好能从镜子里看到旗杆的顶端E,测得脚掌中心位置B到镜面中心C的距离是50cm,镜面中心C距离旗杆底部D的距离为4m,已知淇淇同学的身高是1.54m,眼睛位置A距离淇淇头顶的距离是4cm,求旗杆DE 的高度.

如图2所示,嘉嘉在某一时刻测得 1 米长的竹竿竖直放置时影长2米,在同时刻测量旗杆的影长时,旗杆的影子一部分落在地面上(BC),另一部分落在斜坡上(CD),他测得落在地面上的影长为10米,落在斜坡上的影长为![]() 米,∠DCE=45°,求旗杆AB的高度?
米,∠DCE=45°,求旗杆AB的高度?

查看答案和解析>>
科目:初中数学 来源: 题型:
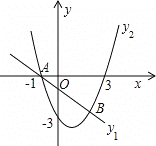
【题目】如图,A(﹣1,0)、B(2,﹣3)两点在一次函数y1=﹣x+m与二次函数y2=ax2+bx﹣3的图象上.
(1)求m的值和二次函数的解析式.
(2)请直接写出使y1>y2时自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
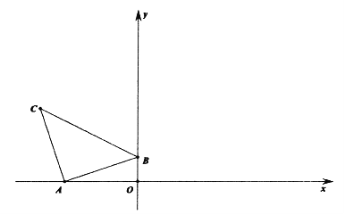
【题目】如图,在平面直角坐标系中有Rt△ABC,∠BAC=90°,AB=AC,A(-3,0),B(0,1),C(m,n)。
(1)请直接写出C点坐标。
(2)将△ABC 沿x轴的正方向平移t个单位,![]() 、
、![]() 两点的对应点、正好落在反比例函数
两点的对应点、正好落在反比例函数![]() 在第一象限内图象上。请求出t,k的值。
在第一象限内图象上。请求出t,k的值。
(3)在(2)的条件下,问是否存x轴上的点M和反比例函数![]() 图象上的点N,使得以
图象上的点N,使得以![]() 、
、![]() 、M、N为顶点的四边形构成平行四边形?如果存在,请求出所有满足条件的点M和点N的坐标;如果不存在,请说明理由。
、M、N为顶点的四边形构成平行四边形?如果存在,请求出所有满足条件的点M和点N的坐标;如果不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com