
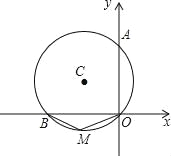
【题目】如图,⊙C 经过原点且与两坐标轴分别交于点 A 与点 B,点 B 的坐标为(﹣![]() ,0),M 是圆上一点,∠BMO=120°.⊙C 圆心 C 的坐标是_____.
,0),M 是圆上一点,∠BMO=120°.⊙C 圆心 C 的坐标是_____.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
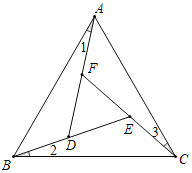
【题目】如图,在等边△ABC中,过A,B,C三点在三角形内分别作∠1=∠2=∠3,三个角的边相交于D,E,F,
(1)你认为△DEF是什么三角形?并证明你的结论;
(2)当∠1,∠2,∠3三个角同时逐渐增大仍保持相等时,△DEF会发生什么变化?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B,C三点在同一直线上,分别以AB,BC(AB>BC)为边,在直线AC的同侧作等边ΔABD和等边ΔBCE,连接AE交BD于点M,连接CD交BE于点N,连接MN. 以下结论:①AE=DC,②MN//AB,③BD⊥AE,④∠DPM=60°,⑤ΔBMN是等边三角形.其中正确的是__________(把所有正确的序号都填上).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解,补全证明过程及推理依据.
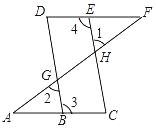
已知:如图,点E在直线DF上,点B在直线AC上,∠1=∠2,∠3=∠4.
求证∠A=∠F
证明:∵∠1=∠2(已知)
∠2=∠DGF( )
∴∠1=∠DGF(等量代换)
∴ ∥ ( )
∴∠3+∠ =180°( )
又∵∠3=∠4(已知)
∴∠4+∠C=180°(等量代换)
∴ ∥ ( )
∴∠A=∠F( )
查看答案和解析>>
科目:初中数学 来源: 题型:
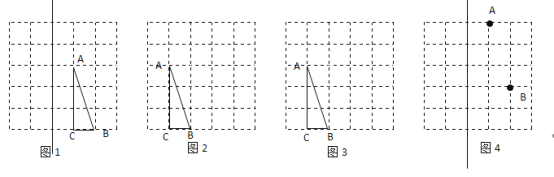
【题目】如图是由边长为![]() 的小正方形构成的网格,每个小正方形的顶点叫做格点,
的小正方形构成的网格,每个小正方形的顶点叫做格点,![]() 的顶点在格点.请选择适当的格点用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由.
的顶点在格点.请选择适当的格点用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由.
(1)如图![]() ,作
,作![]() 关于直线
关于直线![]() 的对称图形
的对称图形![]() ;
;
(2)如图![]() ,作
,作![]() 的高
的高![]() ;
;
(3)如图![]() ,作
,作![]() 的中线
的中线![]() ;
;
(4)如图![]() ,在直线
,在直线![]() 上作出一条长度为
上作出一条长度为![]() 个单位长度的线段
个单位长度的线段![]() 在
在![]() 的上方
的上方![]() ,使
,使![]() 的值最小.
的值最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的正方形网格中,每一个小正方形的边长均为 1.格点三角形 ABC(顶点是网格线交点的三角形)的顶点 A、C 的坐标分别是(﹣2,0),(﹣3,3).
(1)请在图中的网格平面内建立平面直角坐标系,写出点 B 的坐标;
(2)把△ABC 绕坐标原点 O 顺时针旋转 90°得到△A1B1C1,画出△A1B1C1,写出点
B1的坐标;
(3)以坐标原点 O 为位似中心,相似比为 2,把△A1B1C1 放大为原来的 2 倍,得到△A2B2C2 画出△A2B2C2,使它与△AB1C1 在位似中心的同侧;
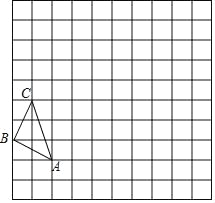
请在 x 轴上求作一点 P,使△PBB1 的周长最小,并写出点 P 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
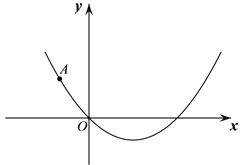
【题目】在平面直角坐标系xOy中,抛物线![]() 经过点A(-3,4).
经过点A(-3,4).
(1)求b的值;
(2)过点A作![]() 轴的平行线交抛物线于另一点B,在直线AB上任取一点P,作点A关于直线OP的对称点C;
轴的平行线交抛物线于另一点B,在直线AB上任取一点P,作点A关于直线OP的对称点C;
①当点C恰巧落在![]() 轴时,求直线OP的表达式;
轴时,求直线OP的表达式;
②连结BC,求BC的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区准备五一组织社区内老年人去到县参加采摘节,现有甲、乙两家旅行社表示对老年人优惠,甲旅行社的优惠方式为:在原来每人100元的基础上,每人按照原价的60%收取费用;乙旅行社的优惠方式为:在收取一个600元固定团费的基础上,再额外收取每人40元.设参加采摘节的老年人有x人,甲、乙两家旅行社实际收费为![]() 元、
元、![]() 元.
元.
(Ⅰ)根据题意,填写下表:
老年人数量(人) | 5 | 10 | 20 | |
甲旅行社收费(元) | 300 | |||
乙旅行社收费)(元) | 800 |
(Ⅱ)求![]() 、
、![]() 关于x的函数关系式(不用写出自变量的取值范围)?
关于x的函数关系式(不用写出自变量的取值范围)?
(Ⅲ)如果![]() ,选择哪家旅行社合算?
,选择哪家旅行社合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com