
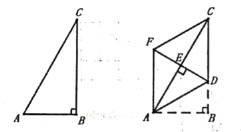
【题目】如图,在![]() 中,
中,![]() .将
.将![]() 向上翻折,使点
向上翻折,使点![]() 落在
落在![]() 上,记为点
上,记为点![]() ,折痕为
,折痕为![]() ,再将
,再将![]() 以
以![]() 为对称轴翻折至
为对称轴翻折至![]() ,连接
,连接![]() .
.
(1)证明:![]()
(2)猜想四边形![]() 的形状并证明.
的形状并证明.
【答案】(1)见解析;(2)四边形ADCF为菱形,证明见解析.
【解析】
(1)根据翻折的性质,先得出AB=AE,∠AED=90°,再根据AC=2AB,可得出DE垂直平分AC,从而可得出结论;
(2)根据折叠的性质以及等边对等角,先求出∠1=∠2=∠3=∠4=30°,从而可得出∠FAB=90°,进而推出AF∥CD,再由边的等量关系,可证明四边形ADCF为菱形.
(1)证明:由轴对称得性质得,
∠B=90°=∠AED,AE=AB,
∵AC =2AB,
∴ED为AC的垂直平分线,
∴AD=CD;
(2)解:四边形ADCF为菱形.证明如下:
∵AD=CD,∴∠1=∠2.
由轴对称性得,
∠1=∠3,∠1=∠4.
∵∠B=90°,
∴∠1=∠2=∠3=∠4=30°,
∴∠FAB=90°,
∴AF∥CD,AF=AD=CD,
∴四边形ADCF为菱形.



科目:初中数学 来源: 题型:
【题目】如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,

(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
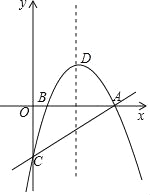
【题目】如图,抛物线y=ax2+bx+c与x轴交于A,B(1,0)两点,与y轴交于点C,直线y=![]() x﹣2经过A,C两点,抛物线的顶点为D.
x﹣2经过A,C两点,抛物线的顶点为D.
(1)求抛物线的解析式及顶点D的坐标;
(2)在直线AC上方的抛物线上存在一点P,使△PAC的面积最大,请直接写出P点坐标及△PAC面积的最大值;
(3)在y轴上是否存在一点G,使得GD+GB的值最小?若存在,求出点G的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料,再解答下列问题:
题:分解因式:![]()
解:将“![]() ”看成整体,设
”看成整体,设![]() ,则原式=
,则原式=![]()
![]()
再将“![]() ”还原,得原式=
”还原,得原式=![]() .
.
上述解题用到的是“整体思想”,“整体思想”是数学解题中常用的一种思想方法,请你仿照上面的方法解答下列问题:
(1)因式分解:![]() ;
;![]() .
.
(2)因式分解:![]() ;
;![]() .
.
(3)求证:若![]() 为正整数,则式子
为正整数,则式子![]() 的值一定是某一个正整数的平方.
的值一定是某一个正整数的平方.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】制文中学2019年秋季在政大商场购进了![]() 、
、![]() 两种品牌的冰鞋,购买
两种品牌的冰鞋,购买![]() 品牌冰鞋花费了
品牌冰鞋花费了![]() 元,购买
元,购买![]() 品牌冰鞋花费了
品牌冰鞋花费了![]() 元,且购买
元,且购买![]() 品牌冰鞋的数量是购买
品牌冰鞋的数量是购买![]() 品牌冰鞋数量的
品牌冰鞋数量的![]() 倍,已知购买一双
倍,已知购买一双![]() 品牌冰鞋比购买一双
品牌冰鞋比购买一双![]() 品牌冰鞋多花
品牌冰鞋多花![]() 元.
元.
(1)求购买一双![]() 品牌,一双
品牌,一双![]() 品牌的冰鞋各需多少元?
品牌的冰鞋各需多少元?
(2)为开展好“冰雪进校园”活动,制文中学决定再次购买两种品牌冰鞋共![]() 双,如果这所中学这次购买
双,如果这所中学这次购买![]() 、
、![]() 两种品牌冰鞋的总费用不超过
两种品牌冰鞋的总费用不超过![]() 元,那么制文中学最多购买多少双
元,那么制文中学最多购买多少双![]() 品牌冰鞋?
品牌冰鞋?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是__________

查看答案和解析>>
科目:初中数学 来源: 题型:
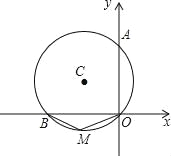
【题目】如图,⊙C 经过原点且与两坐标轴分别交于点 A 与点 B,点 B 的坐标为(﹣![]() ,0),M 是圆上一点,∠BMO=120°.⊙C 圆心 C 的坐标是_____.
,0),M 是圆上一点,∠BMO=120°.⊙C 圆心 C 的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2﹣4x+c经过点A(2,0).
(1)求抛物线的解析式和顶点坐标;
(2)若点B(m,n)是抛物线上的一动点,点B关于原点的对称点为C.
①若B、C都在抛物线上,求m的值;
②若点C在第四象限,当AC2的值最小时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】路边有一根电线杆AB和一块正方形广告牌,有一天,小明突然发现在太阳光照射下,电线杆顶端A的影子刚好落在正方形广告牌B的上边中点G处,而正方形广告牌的影子刚好落在地面上E点(如图),已知BC=5米,正方形边长为3米,DE=4米,则此时电线杆的高度约是( )
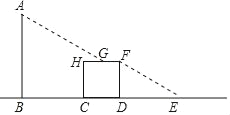
A. 8米 B. 7米 C. 6米 D. 7.9米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com