
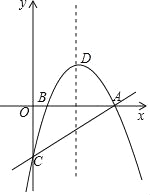
【题目】如图,抛物线y=ax2+bx+c与x轴交于A,B(1,0)两点,与y轴交于点C,直线y=![]() x﹣2经过A,C两点,抛物线的顶点为D.
x﹣2经过A,C两点,抛物线的顶点为D.
(1)求抛物线的解析式及顶点D的坐标;
(2)在直线AC上方的抛物线上存在一点P,使△PAC的面积最大,请直接写出P点坐标及△PAC面积的最大值;
(3)在y轴上是否存在一点G,使得GD+GB的值最小?若存在,求出点G的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+
x2+![]() x﹣2;D(
x﹣2;D(![]() ,
,![]() );(2)P(2,1);△PAC的面积最大为4;(3)存在;G(0,
);(2)P(2,1);△PAC的面积最大为4;(3)存在;G(0,![]() ).
).
【解析】
(1)利用一次函数是性质求得点A、C的坐标,然后把点A、B、C的坐标分别代入二次函数解析式,利用待定系数法求得二次函数解析式即可;将二次函数解析式转化为顶点式方程,可以直接得到答案;
(2)利用分割法求得△PAC的面积为二次函数的形式,利用二次函数最值的求法进行解答;
(3)利用轴对称-最短路径方法证得点G,结合一次函数图象上点的坐标特征求得点G的坐标.
(1)把x=0代入y=![]() x﹣2中得:y=﹣2,
x﹣2中得:y=﹣2,
把y=0代入y=![]() x﹣2中得:x=4,
x﹣2中得:x=4,
∴A(4,0),C(0,﹣2),
把A(4,0),B(1,0),C(0,﹣2)分别代入y=ax2+bx+c,得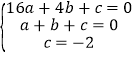 ,
,
解得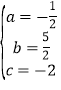 .
.
则该抛物线的解析式为:y=﹣![]() x2+
x2+![]() x﹣2,
x﹣2,
∴y=﹣![]() x2+
x2+![]() x﹣2=﹣
x﹣2=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
∴顶点D(![]() ,
,![]() );
);
(2)在直线AC的上方抛物线上存在点P(2,1),使△PAC的面积最大,最大值为4.理由如下:
如图1,过点P作PQ∥y轴交AC于Q,连接PC,PA.
设P(x,﹣![]() x2+
x2+![]() x﹣2),则Q(x,
x﹣2),则Q(x,![]() x﹣2).
x﹣2).
∴PQ=﹣![]() x2+
x2+![]() x﹣2﹣(
x﹣2﹣(![]() x﹣2)=﹣
x﹣2)=﹣![]() x2+2x=﹣
x2+2x=﹣![]() (x﹣2)2+2.
(x﹣2)2+2.
又∵S△PAC=S△PQC+S△PQA
=![]() xPQ+
xPQ+![]() (4﹣x)PQ
(4﹣x)PQ
=2PQ,
∴S△PAC=﹣(x﹣2)2+4.
∴当x=2时,S△PAC最大值为4,此时﹣![]() x2+
x2+![]() x﹣2=1,
x﹣2=1,
∴在直线AC的上方抛物线上存在点P(2,1),使△PAC的面积最大,最大值为4;
(3)存在点G(0,![]() )使得GD+GB的值最小.理由如下:
)使得GD+GB的值最小.理由如下:
如图1,
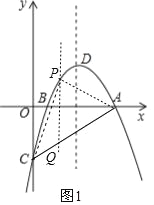
作点B关于y轴的对称点B′,连接B′D交y轴于点G,则B′(﹣1,0),
设直线B′D的解析式为y=kx+b,
则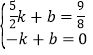 ,解得:
,解得: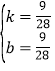 ,
,
∴直线B′D的解析式为y=![]() x+
x+![]() ,
,
把x=0代入,得y=![]() ,
,
∴存在点G(0,![]() )使得GD+GB的值最小.
)使得GD+GB的值最小.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】2019年,在新泰市美丽乡村建设中,甲、乙两个工程队分别承担某处村级道路硬化和道路拓宽改造工程.己知道路硬化和道路拓宽改造工程的总里程数是8.6千米,其中道路硬化的里程数是道路拓宽里程数的2倍少1千米.
(1)求道路硬化和道路拓宽里程数分别是多少千米;
(2)甲、乙两个工程队同时开始施工,甲工程队比乙工程队平均每天多施工10米.由于工期需要,甲工程队在完成所承担的![]() 施工任务后,通过技术改进使工作效率比原来提高了
施工任务后,通过技术改进使工作效率比原来提高了![]() .设乙工程队平均每天施工
.设乙工程队平均每天施工![]() 米,若甲、乙两队同时完成施工任务,求乙工程队平均每天施工的米数
米,若甲、乙两队同时完成施工任务,求乙工程队平均每天施工的米数![]() 和施工的天数.
和施工的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
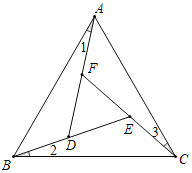
【题目】如图,在等边△ABC中,过A,B,C三点在三角形内分别作∠1=∠2=∠3,三个角的边相交于D,E,F,
(1)你认为△DEF是什么三角形?并证明你的结论;
(2)当∠1,∠2,∠3三个角同时逐渐增大仍保持相等时,△DEF会发生什么变化?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
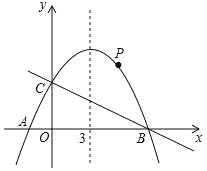
【题目】如图,已知抛物线y=ax2+![]() x+4的对称轴是直线x=3,且与轴相交于A、B两点(B点在A点的右侧),与轴交于C点.
x+4的对称轴是直线x=3,且与轴相交于A、B两点(B点在A点的右侧),与轴交于C点.
(1)A点的坐标是 ;B点坐标是 ;
(2)直线BC的解析式是: ;
(3)点P是直线BC上方的抛物线上的一动点(不与B、C重合),是否存在点P,使△PBC的面积最大.若存在,请求出△PBC的最大面积,若不存在,试说明理由;
(4)若点M在x轴上,点N在抛物线上,以A、C、M、N为顶点的四边形是平行四边形时,请直接写出点M点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中AB=AC,△AED中AE=AD,∠EAD=∠BAC,AC与BD交于点O.
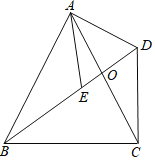
(1)试确定∠ADC与∠AEB间的数量关系,并说明理由;
(2)若∠ACB=65°,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )

A. ①②③④ B. ①④ C. ②③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B,C三点在同一直线上,分别以AB,BC(AB>BC)为边,在直线AC的同侧作等边ΔABD和等边ΔBCE,连接AE交BD于点M,连接CD交BE于点N,连接MN. 以下结论:①AE=DC,②MN//AB,③BD⊥AE,④∠DPM=60°,⑤ΔBMN是等边三角形.其中正确的是__________(把所有正确的序号都填上).

查看答案和解析>>
科目:初中数学 来源: 题型:
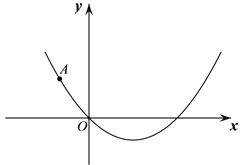
【题目】在平面直角坐标系xOy中,抛物线![]() 经过点A(-3,4).
经过点A(-3,4).
(1)求b的值;
(2)过点A作![]() 轴的平行线交抛物线于另一点B,在直线AB上任取一点P,作点A关于直线OP的对称点C;
轴的平行线交抛物线于另一点B,在直线AB上任取一点P,作点A关于直线OP的对称点C;
①当点C恰巧落在![]() 轴时,求直线OP的表达式;
轴时,求直线OP的表达式;
②连结BC,求BC的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com