
【题目】如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,

(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
【答案】(1)证明见解析(2)4
【解析】解:(1)证明:∵∠APC和∠ABC是同弧所对的圆周角,∴∠APC=∠ABC。
又∵在△ABC中,∠BAC=∠APC=60°,∴∠ABC=60°。
∴∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣60°﹣60°=60°。
∴△ABC是等边三角形。
(2)连接OB,
∵△ABC为等边三角形,⊙O为其外接圆,
∴O为△ABC的外心。
∴BO平分∠ABC。∴∠OBD=30°.∴OD=8×![]() =4。
=4。
(1)根据同弧所对的圆周角相等的性质和已知∠BAC=∠APC=60°可得△ABC的每一个内角都等于600,从而得证。
(2)根据等边三角形三线合一的性质,得含30度角直角三角形OBD,从而根据30度角所对边是斜边一半的性质,得OD=8×![]() =4
=4


科目:初中数学 来源: 题型:
【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.
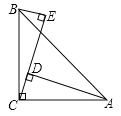
(1)直线BE与AD的位置关系是 ;BE与AD之间的距离是线段 的长;
(2) 若AD=6cm,BE=2cm.,求BE与AD之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.
①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,△ABC的三个顶点在互相平行的三条直线l1,l2,l3上,且l1,l2之间的距离是1,l2,l3之间的距离是2,则BC的长度为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】基本事实:两角及其夹边分别相等的两个三角形全等(简称![]() ).请你在此基础上解决下面问题:
).请你在此基础上解决下面问题:

(1)叙述三角形全等的判定方法中的![]() ;
;
(2)证明![]() .要求:叙述要用文字表达;用图形中的符号表达已知、求证,并证明,证明时各步骤要注明依据.
.要求:叙述要用文字表达;用图形中的符号表达已知、求证,并证明,证明时各步骤要注明依据.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透光的布袋里放入标有数字2,0,﹣3的三张的卡片(形状与质地完全相同).现在随机地抽出两张卡片,将两个数字分别记作某个点的横坐标与纵坐标.
(1)从布袋中同时抽取两张卡片时组成的所有点中,直接写出“点落入第四象限”概率是 ;
(2)如果抽出第一张卡片记录数字后放回布袋,再从袋中抽取第二张卡片记录数字后组成一个点,用画树状图或列表法,求出“点落在坐标轴上”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com