【题目】如图，在△ABC中，AD是BC上的高，tanB=cos∠DAC．
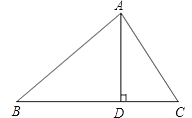
（1）求证：AC=BD；
（2）若sin∠C=
，BC=12，求AD的长．
【答案】（1）证明见解析（2）8
【解析】试题分析：（1）由于tanB=cos∠DAC，所以根据正切和余弦的概念证明AC=BD；
（2）设AD=12k，AC=13k，然后利用题目已知条件解直角三角形即可．
试题解析：解：（1）∵AD是BC上的高，∴AD⊥BC，∴∠ADB=90°，∠ADC=90°．在Rt△ABD和Rt△ADC中，∵tanB=
，cos∠DAC=
，tanB=cos∠DAC，∴
=
，∴AC=BD．
（2）在Rt△ADC中，sinC=
，故可设AD=12k，AC=13k，∴CD=
=5k，∵BC=BD+CD，AC=BD，∴BC=13k+5k=18k．由已知BC=12，∴18k=12，∴k=
，∴AD=12k=12×
=8．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】如图，已知轮船A在灯塔P的北偏东30°的方向上，轮船B在灯塔P的南偏东70°的方向上．
（1）求从灯塔P看两轮船的视角（即∠APB）的度数？
（2）轮船C在∠APB的角平分线上，则轮船C在灯塔P的什么方位？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠ACB=90°，AC=BC，延长AB至点D，使DB=AB，连接CD，以CD为边作△CDE，其中CD=CE，∠DCE=90°，连接BE．
(1)求证：△ACD≌△BCE.
(2)若AB=6cm，则BE=______cm．
(3)BE与AD有何位置关系？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】探索n×n的正方形钉子板上(n是钉子板每边上的钉子数,每边上相邻钉子间的距离为1),连接任意两个钉子所得到的不同长度值的线段种数:
当n=2时,钉子板上所连不同线段的长度值只有1与
，所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
当n=3时,钉子板上所连不同线段的长度值只有1, 
，2, 
，2
五种,比n=2时增加了3种,即S=2+3=5.
(1)观察图形,填写下表:
钉子数(n×n) | S值 |
2×2 | 2 |
3×3 | 2+3 |
4×4 | 2+3+（____） |
5×5 | （________） |
(2)写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可).
(3)对n×n的钉子板,写出用n表示S的代数式.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】 某学校为了改善办学条件，计划采购A，B两种型号的空调，已知采购3台A型空调和2台B型空调共需3.9万元；采购4台A型空调比采购5台B空调的费用多0.6万元．
（1）求A型空调和B型空调每台各需多少万元；
（2）若学校计划采购A，B两种型号空调共30台，且采购总费用不少于20万元不足21万元，请求出共有那些采购方案．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线y＝x＋2与抛物线y＝ax2＋bx＋6(a≠0)相交于点A(
， 
)，B(4，m)，点P是线段AB上异于A，B的动点，过点P作PC⊥x轴于点D，交抛物线于点C.
(1)求抛物线的解析式；
(2)是否存在这样的P点，使线段PC的长有最大值？若存在，求出这个最大值；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在三角形ABC中，AB=6，AC=BC=5，以BC为直径作⊙O交AB于点D，交AC于点G，直线DF是⊙O的切线，D为切点，交CB的延长线于点E．
（1）求证：DF⊥AC；
（2）求tan∠E的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠ACB=90°，∠A=40°，△ABC的外角∠CBD的平分线BE交AC的延长线于点E．
（1）求∠CBE的度数；
（2）过点D作DF∥BE，交AC的延长线于点F，求∠F的度数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
