
【题目】如图,在三角形ABC中,AB=6,AC=BC=5,以BC为直径作⊙O交AB于点D,交AC于点G,直线DF是⊙O的切线,D为切点,交CB的延长线于点E.
(1)求证:DF⊥AC;
(2)求tan∠E的值.

【答案】(1)证明见解析;(2)tan∠CBG=![]() .
.
【解析】(1)连接OC,CD,根据圆周角定理得∠BDC=90°,由等腰三角形三线合一的性质得:D为AB的中点,所以OD是中位线,由三角形中位线性质得:OD∥AC,根据切线的性质可得结论;
(2)如图,连接BG,先证明EF∥BG,则∠CBG=∠E,求∠CBG的正切即可.
(1)证明:如图,连接OC,CD,
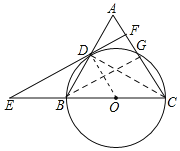
∵BC是⊙O的直径,
∴∠BDC=90°,
∴CD⊥AB,
∵AC=BC,
∴AD=BD,
∵OB=OC,
∴OD是△ABC的中位线
∴OD∥AC,
∵DF为⊙O的切线,
∴OD⊥DF,
∴DF⊥AC;
(2)解:如图,连接BG,
∵BC是⊙O的直径,
∴∠BGC=90°,
∵∠EFC=90°=∠BGC,
∴EF∥BG,
∴∠CBG=∠E,
Rt△BDC中,∵BD=3,BC=5,
∴CD=4,
S△ABC=![]() ,
,
6×4=5BG,
BG=![]() ,
,
由勾股定理得:CG=![]() ,
,
∴tan∠CBG=tan∠E=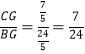 .
.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 一组数据2,2,3,4,这组数据的中位数是2
B. 了解一批灯泡的使用寿命的情况,适合抽样调查
C. 小明的三次数学成绩是126分,130分,136分,则小明这三次成绩的平均数是131分
D. 某日最高气温是![]() ,最低气温是
,最低气温是![]() ,则该日气温的极差是
,则该日气温的极差是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O.△ADE的周长为6cm.

(1)求BC的长;
(2)分别连结OA、OB、OC,若△OBC的周长为16cm,求OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )

A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
C. 三角形三条角平分线的交点到三条边的距离相等
D. 以上均不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题.
(1)初三(1)班接受调查的同学共有多少名;
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;
(3)若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
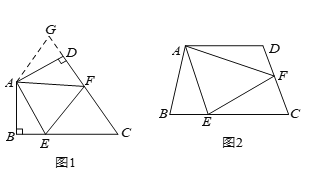
【题目】如图(![]() ),在四边形
),在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,且
上的点,且![]() .探究图中线段
.探究图中线段![]() ,
,![]() ,
,![]() 之间的数量关系.小王同学探究此问题的方法是,延长
之间的数量关系.小王同学探究此问题的方法是,延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() ,先证明
,先证明![]() ≌
≌![]() ,再证明
,再证明![]() ≌
≌![]() ,可得出结论,他的结论应该是__________.
,可得出结论,他的结论应该是__________.
如图(![]() ),若在四边形
),若在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,且
上的点,且![]() ,上述结论是否仍然成立,并说明理由.
,上述结论是否仍然成立,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com