
【题目】在不透光的布袋里放入标有数字2,0,﹣3的三张的卡片(形状与质地完全相同).现在随机地抽出两张卡片,将两个数字分别记作某个点的横坐标与纵坐标.
(1)从布袋中同时抽取两张卡片时组成的所有点中,直接写出“点落入第四象限”概率是 ;
(2)如果抽出第一张卡片记录数字后放回布袋,再从袋中抽取第二张卡片记录数字后组成一个点,用画树状图或列表法,求出“点落在坐标轴上”的概率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)列表表示出“不放回”的取两次的所有结果,再根据概率公式求解可得;
(2)列表表示出“有放回”的取两次的所有结果,再根据概率公式求解可得.
(1)列表如下:
2 | 0 | ﹣3 | |
2 | (0,2) | (﹣3,2) | |
0 | (2,0) | (﹣3,0) | |
﹣3 | (2,﹣3) | (0,﹣3) |
由表可知共有6种等可能结果,其中“点落入第四象限”的有1种结果,
所以“点落入第四象限”的概率为![]() ,
,
故答案为:![]() ;
;
(2)列表如下:
2 | 0 | ﹣3 | |
2 | (2,2) | (0,2) | (﹣3,2) |
0 | (2,0) | (0,0) | (﹣3,0) |
﹣3 | (2,﹣3) | (0,﹣3) | (﹣3,﹣3) |
由表可知,共有9种等可能结果,其中“点落在坐标轴上”的有5种结果,
所以“点落在坐标轴上”的概率为![]() .
.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:
【题目】如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,

(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,以点A为圆心,小于AC的长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,以大于![]() EF长为半径作圆弧,两条弧交于点G,作射线AG交CD于点H,若∠C=120°,则∠AHD=( )
EF长为半径作圆弧,两条弧交于点G,作射线AG交CD于点H,若∠C=120°,则∠AHD=( )

A. 120° B. 30° C. 150° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=ax2+bx经过点A(2,4)和点B(6,0).
(1)求这条抛物线所对应的二次函数的解析式;
(2)直接写出它的开口方向、顶点坐标;
(3)点(x1,y1),(x2,y2)均在此抛物线上,若x1>x2>4,则y1 ________ y2(填“>”“=”或“<”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】双十一购物节即将到来,某商场设计了两种的促销方案,并有以下两种销售量预期.预期一:第1步,销售量扩大为原来的a倍.第2步,再扩大为第1步销售量的b倍.预期二:第1步,销售量扩大为原来的![]() 倍;第2步,再扩大为第1步销售量的
倍;第2步,再扩大为第1步销售量的![]() 倍;其中a,b为不相等的正数,请问两种预期中,哪种销售量更多?试说明理由.
倍;其中a,b为不相等的正数,请问两种预期中,哪种销售量更多?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是2018年三月份某居民小区随机抽取20户居民的用水情况:
月用水量/吨 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
户数 | 2 | 4 | m | 4 | 3 | 0 | 1 |
(1)求出m= ,补充画出这20户家庭三月份用电量的条形统计图;
(2)据上表中有关信息,计算或找出下表中的统计量,并将结果填入表中:
统计量名称 | 众数 | 中位数 | 平均数 |
数据 |
|
|
|
(3)为了倡导“节约用水,绿色环保”的意识,江赣市自来水公司实行“梯级用水、分类计费”,价格表如下:
月用水梯级标准 | Ⅰ级(30吨以内) | Ⅱ级(超过30吨的部分) |
单价(元/吨) | 2.4 | 4 |
如果该小区有500户家庭,根据以上数据,请估算该小区三月份有多少户家庭达到Ⅱ级标准?并估算这些Ⅱ级用水户的总水费是多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线L1:y=﹣x2+2x+3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,在L1上任取一点P,过点P作直线l⊥x轴,垂足为D,将L1沿直线l翻折得到抛物线L2,交x轴于点M,N(点M在点N的左侧).
(1)当L1与L2重合时,求点P的坐标;
(2)当点P与点B重合时,求此时L2的解析式;并直接写出L1与L2中,y均随x的增大而减小时的x的取值范围;
(3)连接PM,PB,设点P(m,n),当n=![]() m时,求△PMB的面积.
m时,求△PMB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,且AB=6cm,则△DEB的周长为( )
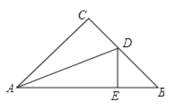
A. 4cm B. 6cm C. 8cm D. 10cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB上一点,AE=AD,且BF∥CD,AF⊥CE的延长线于F.连接DE交对角线AC于H.下列结论:①AC垂直平分ED;②AE=BE;③CE=2BF;④BE=2EF.其中结论正确的是_______.(填序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com