
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,△ABC的三个顶点在互相平行的三条直线l1,l2,l3上,且l1,l2之间的距离是1,l2,l3之间的距离是2,则BC的长度为_____.

【答案】2![]() .
.
【解析】
过点B作BE⊥l1于点E,过点C作CF⊥l1于点F,由余角的性质可得∠CAF=∠BAE,由“AAS”可证△ABE≌△CAF,可得AE=CF=1,由勾股定理可求AB的长,BC的长.
解:如图,过点B作BE⊥l1于点E,过点C作CF⊥l1于点F,
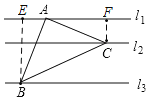
∵l1,l2之间的距离是1,l2,l3之间的距离是2,
∴BE=3,CF=1,
∵∠BAC=90°,BE⊥AF
∴∠BAE+∠CAF=90°,∠BAE+∠ABE=90°
∴∠CAF=∠BAE,且AB=AC,∠AEB=∠AFC=90°
∴△ABE≌△CAF(AAS)
∴AE=CF=1,
∴在Rt△ABE中,AB=![]() =
=![]()
∵∠BAC=90°,AB=AC
∴BC=![]() AB=2
AB=2![]()
故答案为:2![]()


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(2m+1)x+m(m+1)=0,
(1)求证:方程总有两个不相等的实数根;
(2)设方程的两根分别为x1、x2,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,

(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.
(1)请你用直尺和圆规作出这个输水管道的圆形截面的圆心(保留作图痕迹);
(2)若这个输水管道有水部分的水面宽AB=8 cm,水面最深地方的高度为2 cm,求这个圆形截面的半径.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象过点A(3,0),对称轴为直线x=1,给出以下结论:①abc<0;②b2﹣4ac>0;③a+b+c≥ax2+bx+c;④若M(x2+1,y1)、N(x2+2,y2)为函数图象上的两点,则y1<y2,其中正确的是( )

A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,以点A为圆心,小于AC的长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,以大于![]() EF长为半径作圆弧,两条弧交于点G,作射线AG交CD于点H,若∠C=120°,则∠AHD=( )
EF长为半径作圆弧,两条弧交于点G,作射线AG交CD于点H,若∠C=120°,则∠AHD=( )

A. 120° B. 30° C. 150° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线L1:y=﹣x2+2x+3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,在L1上任取一点P,过点P作直线l⊥x轴,垂足为D,将L1沿直线l翻折得到抛物线L2,交x轴于点M,N(点M在点N的左侧).
(1)当L1与L2重合时,求点P的坐标;
(2)当点P与点B重合时,求此时L2的解析式;并直接写出L1与L2中,y均随x的增大而减小时的x的取值范围;
(3)连接PM,PB,设点P(m,n),当n=![]() m时,求△PMB的面积.
m时,求△PMB的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com