
【题目】已知抛物线y=﹣x2﹣4x+c经过点A(2,0).
(1)求抛物线的解析式和顶点坐标;
(2)若点B(m,n)是抛物线上的一动点,点B关于原点的对称点为C.
①若B、C都在抛物线上,求m的值;
②若点C在第四象限,当AC2的值最小时,求m的值.
【答案】(1)抛物线解析式为y=﹣x2﹣4x+12,顶点坐标为(﹣2,16);(2)①m=2![]() 或m=﹣2
或m=﹣2![]() ;②m的值为
;②m的值为![]() .
.
【解析】(1)把点A(2,0)代入抛物线y=﹣x2﹣4x+c中求得c的值,即可得抛物线的解析式,根据抛物线的解析式求得抛物线的顶点坐标即可;(2)①由B(m,n)在抛物线上可得﹣m2﹣4m+12=n,再由点B关于原点的对称点为C,可得点C的坐标为(﹣m,﹣n),又因C落在抛物线上,可得﹣m2+4m+12=﹣n,即m2﹣4m﹣12=n,所以﹣m2+4m+12=m2﹣4m﹣12,解方程求得m的值即可;②已知点C(﹣m,﹣n)在第四象限,可得﹣m>0,﹣n<0,即m<0,n>0,再由抛物线顶点坐标为(﹣2,16),即可得0<n≤16,因为点B在抛物线上,所以﹣m2﹣4m+12=n,可得m2+4m=﹣n+12,由A(2,0),C(﹣m,﹣n),可得AC2=(﹣m﹣2)2+(﹣n)2=m2+4m+4+n2=n2﹣n+16=(n﹣![]() )2+
)2+![]() ,所以当n=
,所以当n=![]() 时,AC2有最小值,即﹣m2﹣4m+12=
时,AC2有最小值,即﹣m2﹣4m+12=![]() ,解方程求得m的值,再由m<0即可确定m的值.
,解方程求得m的值,再由m<0即可确定m的值.
(1)∵抛物线y=﹣x2﹣4x+c经过点A(2,0),
∴﹣4﹣8+c=0,即c=12,
∴抛物线解析式为y=﹣x2﹣4x+12=﹣(x+2)2+16,
则顶点坐标为(﹣2,16);
(2)①由B(m,n)在抛物线上可得:﹣m2﹣4m+12=n,
∵点B关于原点的对称点为C,
∴C(﹣m,﹣n),
∵C落在抛物线上,
∴﹣m2+4m+12=﹣n,即m2﹣4m﹣12=n,
解得:﹣m2+4m+12=m2﹣4m﹣12,
解得:m=2![]() 或m=﹣2
或m=﹣2![]() ;
;
②∵点C(﹣m,﹣n)在第四象限,
∴﹣m>0,﹣n<0,即m<0,n>0,
∵抛物线顶点坐标为(﹣2,16),
∴0<n≤16,
∵点B在抛物线上,
∴﹣m2﹣4m+12=n,
∴m2+4m=﹣n+12,
∵A(2,0),C(﹣m,﹣n),
∴AC2=(﹣m﹣2)2+(﹣n)2=m2+4m+4+n2=n2﹣n+16=(n﹣![]() )2+
)2+![]() ,
,
当n=![]() 时,AC2有最小值,
时,AC2有最小值,
∴﹣m2﹣4m+12=![]() ,
,
解得:m=![]() ,
,
∵m<0,∴m=![]() 不合题意,舍去,
不合题意,舍去,
则m的值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】张老师元旦节期间到武商众圆商场购买一台某品牌笔记本电脑,恰逢商场正推出“迎元旦”促销打折活动,具体优惠情况如表:
购物总金额(原价) | 折扣 |
不超过5000元的部分 | 九折 |
超过5000元且不超过10000元的部分 | 八折 |
超过10000元且不超过20000元的部分 | 七折 |
…… | …… |
例如:若购买的商品原价为15000元,实际付款金额为:
5000×90%+(10000﹣5000)×80%+(15000﹣10000)×70%=12000元.
(1)若这种品牌电脑的原价为8000元/台,请求出张老师实际付款金额;
(2)已知张老师购买一台该品牌电脑实际付费5700元.
①求该品牌电脑的原价是多少元/台?
②若售出这台电脑商场仍可获利14%,求这种品牌电脑的进价为多少元/台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察推理:如图1,△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A、B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D、E.
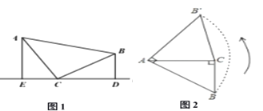
求证:△AEC≌△CDB;
(2)类比探究:如图2,Rt△ABC中,∠ACB=90°,AC=6,将斜边AB绕点A逆时针旋转90°至AB,连接B,C,求△AB,C的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
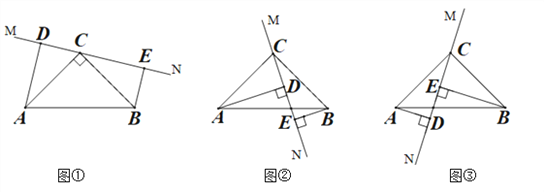
【题目】在△ABC中,∠ACB=90,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图①位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到图②位置时,试问:DE,AD,BE有怎样的等量关系?请写出这个等量关系,并加以证明.
(3)当直线MN绕点C旋转到图③位置时,DE,AD,BE之间的等量关系是 (直接写出答案,不需证明.)
查看答案和解析>>
科目:初中数学 来源: 题型:
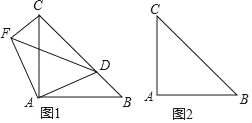
【题目】如图1所示,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为直角边,A为直角顶点,在AD左侧作等腰直角三角形ADF,连接CF,AB=AC,∠BAC=90°.
(1)当点D在线段BC上时(不与点B重合),线段CF和BD的数量关系与位置关系分别是什么?请给予证明.
(2)当点D在线段BC的延长线上时,(1)的结论是否仍然成立?请在图2中画出相应的图形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
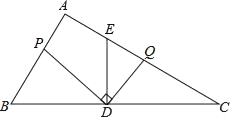
【题目】如图,在Rt△ABC中,∠A=90°,AB=12,AC=16,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上的一动点,点Q为边AC上的一动点,且∠PDQ=90°.
(1)求ED、EC的长;
(2)若BP=2,求CQ的长;
(3)若线段PQ与线段DE的交点为F,当△PDF为等腰三角形时,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中秋节临近,某商场决定开展“金秋十月,回馈顾客”的让利活动,对部分品牌月饼进行打折销售,其中甲品牌月饼打八折,乙品牌月饼打七五折.已知打折前,买![]() 盒甲品牌月饼和
盒甲品牌月饼和![]() 盒乙品牌月饼需
盒乙品牌月饼需![]() 元;打折后,买
元;打折后,买![]() 盒甲品牌月饼和
盒甲品牌月饼和![]() 盒乙品牌月饼需
盒乙品牌月饼需![]() 元.
元.
(1)打折前甲、乙两种品牌月饼每盒分别为多少元?
(2)幸福敬老院需购买甲品牌月饼![]() 盒,乙品牌月饼
盒,乙品牌月饼![]() 盒,问打折后购买这批月饼比不打折节省了多少钱?
盒,问打折后购买这批月饼比不打折节省了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形ABCD中,AB=3,BC=4,动点P从点A开始按A→B→C→D的方向运动到点D.如图,设动点P所经过的路程为x,△APD的面积为y.(当点P与点A或D重合时,y=0)
(1)写出y与x之间的函数解析式;
(2)画出此函数的图象.

查看答案和解析>>
科目:初中数学 来源: 题型:
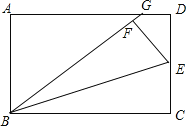
【题目】如图,在矩形ABCD中,点E是CD的中点,将△BCE沿BE折叠后得到△BEF、且点F在矩形ABCD的内部,将BF延长交AD于点G.若![]() ,则
,则![]() =__.
=__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com