
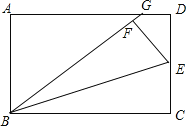
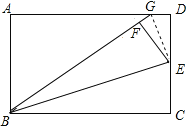
【题目】如图,在矩形ABCD中,点E是CD的中点,将△BCE沿BE折叠后得到△BEF、且点F在矩形ABCD的内部,将BF延长交AD于点G.若![]() ,则
,则![]() =__.
=__.
【答案】![]()
【解析】
连接GE,根据中点定义可得DE=CE,再根据翻折的性质可得DE=EF,∠BFE=90°,利用“HL”证明Rt△EDG≌Rt△EFG,根据全等三角形对应边相等可得FG=DG,根据![]() ,设DG=FG=a,则AG=7a,故AD=BC=8a,则BG=BF+FG=9a,由勾股定理求得AB=
,设DG=FG=a,则AG=7a,故AD=BC=8a,则BG=BF+FG=9a,由勾股定理求得AB=![]() ,再求比值即可.
,再求比值即可.
连接GE,
∵点E是CD的中点,∴EC=DE,
∵将△BCE沿BE折叠后得到△BEF、且点F在矩形ABCD的内部,
∴EF=DE,∠BFE=90°,
在Rt△EDG和Rt△EFG中![]() ,
,
∴Rt△EDG≌Rt△EFG(HL),
∴FG=DG,
∵![]() ,
,
∴设DG=FG=a,则AG=7a,故AD=BC=8a,则BG=BF+FG=9a,
∴AB=![]() ,
,
故![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2﹣4x+c经过点A(2,0).
(1)求抛物线的解析式和顶点坐标;
(2)若点B(m,n)是抛物线上的一动点,点B关于原点的对称点为C.
①若B、C都在抛物线上,求m的值;
②若点C在第四象限,当AC2的值最小时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
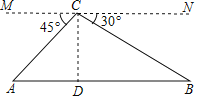
【题目】如图,某景区的两个景点A、B处于同一水平地面上、一架无人机在空中沿MN方向水平飞行进行航拍作业,MN与AB在同一铅直平面内,当无人机飞行至C处时、测得景点A的俯角为45°,景点B的俯角为30°,此时C到地面的距离CD为100米,则两景点A、B间的距离为__米(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
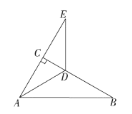
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,试说明DA=DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:
在△ABC中,AB,BC,AC三边的长度分别为![]() ,求这个三角形的面积。
,求这个三角形的面积。
小辉同学在解得这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.

(1)请你直接写出△ABC的面积为:______;
思维拓展
(2)若△DEF三边的长分别为![]() a,2
a,2![]() a,
a,![]() a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC. 并利用构图法求出它的面积;
a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC. 并利用构图法求出它的面积;
探索创新:
(3)若在△ABC三边的长分别为![]() ,
,![]() ,
,![]() (m>0,n>0,且m≠n),试运用构图法求出三角形的面积。
(m>0,n>0,且m≠n),试运用构图法求出三角形的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
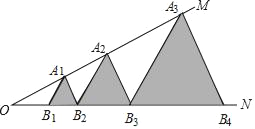
【题目】如图,已知:∠MON=30°,点A1、A2、A3、…在射线ON上,点B1、B2、B3、…在射线OM上,△A1B1B2、△A2B2B3、△A3B3B4、…均为等边三角形,若OB1=1,则△A8B8B9的边长为_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com