
【题目】问题背景:
在△ABC中,AB,BC,AC三边的长度分别为![]() ,求这个三角形的面积。
,求这个三角形的面积。
小辉同学在解得这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.

(1)请你直接写出△ABC的面积为:______;
思维拓展
(2)若△DEF三边的长分别为![]() a,2
a,2![]() a,
a,![]() a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC. 并利用构图法求出它的面积;
a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC. 并利用构图法求出它的面积;
探索创新:
(3)若在△ABC三边的长分别为![]() ,
,![]() ,
,![]() (m>0,n>0,且m≠n),试运用构图法求出三角形的面积。
(m>0,n>0,且m≠n),试运用构图法求出三角形的面积。
科目:初中数学 来源: 题型:
【题目】中秋节临近,某商场决定开展“金秋十月,回馈顾客”的让利活动,对部分品牌月饼进行打折销售,其中甲品牌月饼打八折,乙品牌月饼打七五折.已知打折前,买![]() 盒甲品牌月饼和
盒甲品牌月饼和![]() 盒乙品牌月饼需
盒乙品牌月饼需![]() 元;打折后,买
元;打折后,买![]() 盒甲品牌月饼和
盒甲品牌月饼和![]() 盒乙品牌月饼需
盒乙品牌月饼需![]() 元.
元.
(1)打折前甲、乙两种品牌月饼每盒分别为多少元?
(2)幸福敬老院需购买甲品牌月饼![]() 盒,乙品牌月饼
盒,乙品牌月饼![]() 盒,问打折后购买这批月饼比不打折节省了多少钱?
盒,问打折后购买这批月饼比不打折节省了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
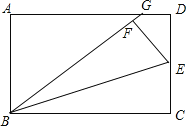
【题目】如图,在矩形ABCD中,点E是CD的中点,将△BCE沿BE折叠后得到△BEF、且点F在矩形ABCD的内部,将BF延长交AD于点G.若![]() ,则
,则![]() =__.
=__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某爱心企业在政府的支持下投入资金,准备修建一批室外简易的足球场和篮球场,供市民免费使用,修建1个足球场和1个篮球场共需8.5万元,修建2个足球场和4个篮球场共需27万元.
(1)求修建一个足球场和一个篮球场各需多少万元?
(2)该企业预计修建这样的足球场和篮球场共20个,投入资金不超过90万元,求至少可以修建多少个足球场?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他费用80元.

(1)请直接写出y与x之间的函数关系式;
(2)如果每天获得160元的利润,销售单价为多少元?
(3)设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
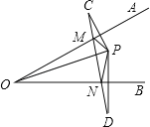
【题目】如图,∠AOB=30°,P是∠AOB内的一点,且OP=4cm,C、D分别是P关于OA、OB的对称点,连结CD、PM、PN,则△PMN的周长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到![]() 的位置,AB=8,DO=2,平移距离为4,则阴影部分面积为( )
的位置,AB=8,DO=2,平移距离为4,则阴影部分面积为( )
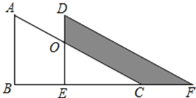
A.28B.40C.42D.48
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 是最小的正整数,且
是最小的正整数,且![]() 、
、![]() 满足
满足![]() ,请回答问题:
,请回答问题:
(1)请直接写出![]() 、
、![]() 、
、![]() 的值:
的值:![]() ________
________![]() ________
________![]() ________;
________;
(2)![]() 、
、![]() 、
、![]() 所对应的点分别为
所对应的点分别为![]() 、
、![]() 、
、![]() ,点
,点![]() 是数轴上的一个动点,其对应的数为
是数轴上的一个动点,其对应的数为![]() ,当
,当![]() 点在0到2之间(即
点在0到2之间(即![]() )运动时,请化简
)运动时,请化简![]() (请写出化简过程);
(请写出化简过程);
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com