
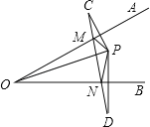
【题目】如图,∠AOB=30°,P是∠AOB内的一点,且OP=4cm,C、D分别是P关于OA、OB的对称点,连结CD、PM、PN,则△PMN的周长为________.
【答案】4cm
【解析】
如图,连接OC、OD,先根据轴对称的性质得出OC=OD=OP,∠COD=2∠AOB=60°,进一步即可判定△OCD是等边三角形,从而可得CD=OC,而易证CD的长就是△PMN的周长,于是问题得解.
解:如图,连接OC、OD,∵C、D分别是点P关于OA、OB的对称点,
∴PM=CM、PN=DN,OC=OD=OP,∠AOP=∠AOC,∠BOP=∠BOD,
∵∠AOB=30°,
∴∠COD=∠AOC+∠AOP+∠BOD+∠BOP=2∠AOB=2×30°=60°,
∴△OCD是等边三角形,
∵OP=4cm,
∴CD=OC=4cm,
∴△PMN的周长=PM+MN+PN=CM+MN+ND=CD=4cm.
故答案为:4cm.


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
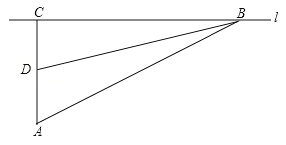
【题目】校车安全是近几年社会关注的热点问题,安全隐患主要是超速和超载.某中学九年级数学活动小组进行了测试汽车速度的实验,如图,先在笔直的公路l旁选取一点A,在公路l上确定点B、C,使得AC⊥l,∠BAC=60°,再在AC上确定点D,使得∠BDC=75°,测得AD=40米,已知本路段对校车限速是50千米/时,若测得某校车从B到C匀速行驶用时10秒,问这辆车在本路段是否超速?请说明理由(参考数据:![]() =1.41,
=1.41,![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
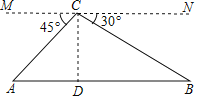
【题目】如图,某景区的两个景点A、B处于同一水平地面上、一架无人机在空中沿MN方向水平飞行进行航拍作业,MN与AB在同一铅直平面内,当无人机飞行至C处时、测得景点A的俯角为45°,景点B的俯角为30°,此时C到地面的距离CD为100米,则两景点A、B间的距离为__米(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:
在△ABC中,AB,BC,AC三边的长度分别为![]() ,求这个三角形的面积。
,求这个三角形的面积。
小辉同学在解得这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.

(1)请你直接写出△ABC的面积为:______;
思维拓展
(2)若△DEF三边的长分别为![]() a,2
a,2![]() a,
a,![]() a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC. 并利用构图法求出它的面积;
a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC. 并利用构图法求出它的面积;
探索创新:
(3)若在△ABC三边的长分别为![]() ,
,![]() ,
,![]() (m>0,n>0,且m≠n),试运用构图法求出三角形的面积。
(m>0,n>0,且m≠n),试运用构图法求出三角形的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
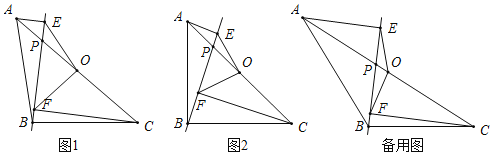
【题目】在△ABC中,AB=BC,点O是AC的中点,点P是AC上的一个动点(点P不与点A,O,C重合).过点A,点C作直线BP的垂线,垂足分别为点E和点F,连接OE,OF.
(1)如图1,请直接写出线段OE与OF的数量关系;
(2)如图2,当∠ABC=90°时,请判断线段OE与OF之间的数量关系和位置关系,并说明理由
(3)若|CF﹣AE|=2,EF=2![]() ,当△POF为等腰三角形时,请直接写出线段OP的长.
,当△POF为等腰三角形时,请直接写出线段OP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
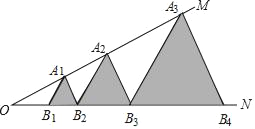
【题目】如图,已知:∠MON=30°,点A1、A2、A3、…在射线ON上,点B1、B2、B3、…在射线OM上,△A1B1B2、△A2B2B3、△A3B3B4、…均为等边三角形,若OB1=1,则△A8B8B9的边长为_____
查看答案和解析>>
科目:初中数学 来源: 题型:
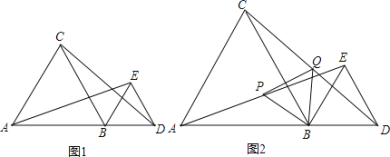
【题目】如图1,点B是线段AD上一点,△ABC和△BDE分别是等边三角形,连接AE和CD.
(1)求证:AE=CD;
(2)如图2,点P、Q分别是AE、CD的中点,试判断△PBQ的形状,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.
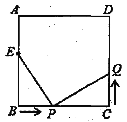
(1)若点Q的运动速度与点P的运动速度相等,经过 秒后,△BPE≌△CQP;
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPE与△CQP全等?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com