
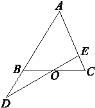
【题目】如图,已知O是△ABC中BC边的中点,且![]() ,则
,则![]() =________.
=________.
【答案】![]()
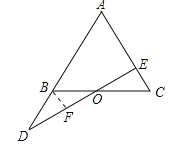
【解析】过B作BF平行于AC,交DE于点F,由两直线平行内错角相等得到两对内错角相等,再由O为BC的中点,得到BO=CO,利用AAS可得出三角形BOF与三角形COE全等,根据全等三角形对应边相等可得出BF=EC,再由BF平行于AE,得到△DBF∽△DAE,利用相似三角形的性质列出比例式,根据已知AB与AD的比值求出BD与AD的比值,即可得到BF与AE的比值,将BF等量代换为EC,可得出EC与AE的比值,根据比例的性质即可求出AE与AC的比值.
过B作BF∥AC,交DE于点F,
∵BF∥AC,∴∠FBO=∠C,∠BFO=∠CEO,
又O为BC的中点,∴BO=CO,
在△OBF和△OCE中,
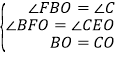 ,∴△OBF≌△OCE(AAS),∴BF=CE,
,∴△OBF≌△OCE(AAS),∴BF=CE,
∵![]() =
=![]() ,∴
,∴![]() =
=![]() ,
,
又∵BF∥AE,∴△DBF∽△DAE,∴![]() =
=![]() =
=![]() =
=![]() ,
,
则![]() =
=![]() =
=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】已知,直线AB∥CD,E为AB、CD间的一点,连接EA、EC.
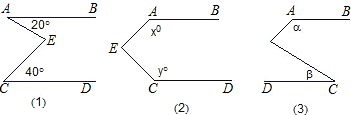
(1)如图①,若∠A=20°,∠C=40°,则∠AEC= °.
(2)如图②,若∠A=x°,∠C=y°,则∠AEC= °.
(3)如图③,若∠A=α,∠C=β,则α,β与∠AEC之间有何等量关系.并简要说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
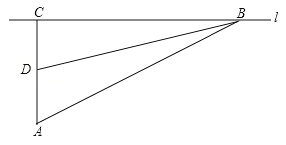
【题目】校车安全是近几年社会关注的热点问题,安全隐患主要是超速和超载.某中学九年级数学活动小组进行了测试汽车速度的实验,如图,先在笔直的公路l旁选取一点A,在公路l上确定点B、C,使得AC⊥l,∠BAC=60°,再在AC上确定点D,使得∠BDC=75°,测得AD=40米,已知本路段对校车限速是50千米/时,若测得某校车从B到C匀速行驶用时10秒,问这辆车在本路段是否超速?请说明理由(参考数据:![]() =1.41,
=1.41,![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
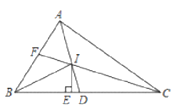
【题目】如图,在△ABC中,AD、CF分别是∠BAC、∠ACB的角平分线,且AD、CF交于点I, IE⊥B于E,下列结论:①∠BIE=∠CID;②S△ABC=![]() IE(AB+BC+AC);③BE=
IE(AB+BC+AC);③BE=![]() (AB+BC-AC);④AC=AF+DC.其中正确的结论是_______________ (填序号)
(AB+BC-AC);④AC=AF+DC.其中正确的结论是_______________ (填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
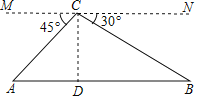
【题目】如图,某景区的两个景点A、B处于同一水平地面上、一架无人机在空中沿MN方向水平飞行进行航拍作业,MN与AB在同一铅直平面内,当无人机飞行至C处时、测得景点A的俯角为45°,景点B的俯角为30°,此时C到地面的距离CD为100米,则两景点A、B间的距离为__米(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:
在△ABC中,AB,BC,AC三边的长度分别为![]() ,求这个三角形的面积。
,求这个三角形的面积。
小辉同学在解得这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.

(1)请你直接写出△ABC的面积为:______;
思维拓展
(2)若△DEF三边的长分别为![]() a,2
a,2![]() a,
a,![]() a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC. 并利用构图法求出它的面积;
a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC. 并利用构图法求出它的面积;
探索创新:
(3)若在△ABC三边的长分别为![]() ,
,![]() ,
,![]() (m>0,n>0,且m≠n),试运用构图法求出三角形的面积。
(m>0,n>0,且m≠n),试运用构图法求出三角形的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求BC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com