
【题目】如图,在△ABC中,AD、CF分别是∠BAC、∠ACB的角平分线,且AD、CF交于点I, IE⊥B于E,下列结论:①∠BIE=∠CID;②S△ABC=![]() IE(AB+BC+AC);③BE=
IE(AB+BC+AC);③BE=![]() (AB+BC-AC);④AC=AF+DC.其中正确的结论是_______________ (填序号)
(AB+BC-AC);④AC=AF+DC.其中正确的结论是_______________ (填序号)
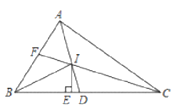
【答案】①②③.
【解析】
如图,作IM⊥AB于M,IN⊥AC于N.根据角平分线的性质定理以及全等三角形的判定和性质一一判断即可;
如图,作IM⊥AB于M,IN⊥AC于N.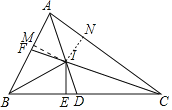
∵AD、CF分别是∠BAC、∠ACB的角平分线,IM⊥AB,IN⊥AC,IE⊥BC,
∴IE=IM=IN,
∴S△ABC=S△ABI+S△ACI+S△BCI=![]() ABIM+
ABIM+![]() ACIN+
ACIN+![]() BCIE=
BCIE=![]() IE(AB+BC+AC),故②正确,
IE(AB+BC+AC),故②正确,
∵∠ABC+∠ACB+∠BAC=180°,∠IBE=![]() ∠ABC,∠IAC=
∠ABC,∠IAC=![]() ∠BAC,∠ICA=
∠BAC,∠ICA=![]() ∠ACB,
∠ACB,
∴∠IBE+∠IAC+∠ICA=90°,
∵∠CID=∠IAC+∠ICA=90°-∠IBE=∠BIE,故①正确,
∵BI=BI,IM=IE,
∴Rt△BIM≌Rt△BIE(HL),
∴BE=BM,同法可证:AM=AN,CN=CE,
∴BE=![]() (AB+BC-AC),故③正确,
(AB+BC-AC),故③正确,
④只有在∠ABC=60°的条件下,AC=AF+DC,故④错误,
故答案为:①②③.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象分别经过点(0,3),(3,0),(4,﹣5).
(1)求这个二次函数的解析式;
(2)求这个二次函数的最值;
(3)若设这个次函数图象与x轴交于点C,D(点C在点D的左侧),且点A是该图象的顶点,请在这个二次函数的对称轴上确定一点B,使△ACB时等腰三角形,求出点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
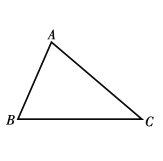
【题目】如图,在![]() 中,
中,![]() 请按要求用尺规作出下列图形(不写作法,但要保留作图痕迹),并填空.
请按要求用尺规作出下列图形(不写作法,但要保留作图痕迹),并填空.
![]() 作出
作出![]() 的平分线交
的平分线交![]() 于点
于点![]() ;
;
![]() 作
作![]() 交
交![]() 于点
于点![]() 平行依据是_____ __;
平行依据是_____ __;
![]() 的度数为 .
的度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
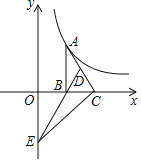
【题目】如图,已知点A在反比例函数y=![]() (x>0)的图象上,作Rt△ABC,边BC在x轴上,点D为斜边AC的中点,连结DB并延长交y轴于点E,若△BCE的面积为4,则k=______.
(x>0)的图象上,作Rt△ABC,边BC在x轴上,点D为斜边AC的中点,连结DB并延长交y轴于点E,若△BCE的面积为4,则k=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
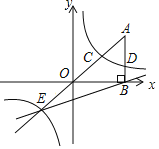
【题目】如图,在平面直角坐标系中,A点的坐标为(a,6),AB⊥x轴于点B,cos∠OAB═![]() ,反比例函数y=
,反比例函数y=![]() 的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为
的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为![]() .
.
(1)求反比例函数的解析式;
(2)求直线EB的解析式;
(3)求S△OEB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=90,A是∠MON内部的一点,过点A作AB⊥ON,垂点为点B,AB=3厘米,OB=4厘米,动点E、F同时从O点出发,点E以1.5厘米/秒的速度沿ON方向运动,点F以2厘米/秒的速度沿OM方向运动,EF与OA交于点C,连接AE,当点E到达点B时,点F随之停止运动。设运动时间为t秒(t>0)。
(1)当t=1秒时,ΔEOF与ΔABO是否相似?请说明理由。
(2)在运动过程中,不论t取何值时,总有EF⊥OA,为什么?
(3)连接AF,在运动过程中,是否存在某一时刻t,使得SΔAEF=![]() S四边形ABOF ?若存在,请求出此时t的值;若不存在,请说明理由。
S四边形ABOF ?若存在,请求出此时t的值;若不存在,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某爱心企业在政府的支持下投入资金,准备修建一批室外简易的足球场和篮球场,供市民免费使用,修建1个足球场和1个篮球场共需8.5万元,修建2个足球场和4个篮球场共需27万元.
(1)求修建一个足球场和一个篮球场各需多少万元?
(2)该企业预计修建这样的足球场和篮球场共20个,投入资金不超过90万元,求至少可以修建多少个足球场?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com