
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD,CE是角平分线,则图中的等腰三角形共有
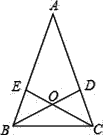
A. 8个 B. 7个 C. 6个 D. 5个
【答案】A
【解析】
根据三角形内角和定理求出∠ABC=∠ACB=72°,根据角平分线求出∠ABD=∠DBC=∠ACE=∠ECB=36°,根据三角形内角和定理求出∠BDC、∠BEC、∠EOB、∠DOC,根据等腰三角形的判定推出即可.
∵AB=AC,∠A=36°,
∴∠ABC=∠ACB=![]() (180°∠A)=72°,
(180°∠A)=72°,
∵BD,CE是角平分线,
∴∠ABD=∠DBC=![]() ∠ABC=36°,∠ACE=∠ECB=36°,
∠ABC=36°,∠ACE=∠ECB=36°,
∴∠A=∠ABD=∠ACE,∠DBC=∠ECB,
∴∠BDC=180°∠ACB∠DBC=180°72°36°=72°,
同理∠BEC=72°,
∴∠BDC=∠ACB,∠BEC=∠EBC,
∴∠EOB=180°∠BEC∠EBD=180°72°36°=72°,
同理∠DOC=72°,
∴∠BEO=∠BOE,∠CDO=∠COD,
即等腰三角形有△OBC,△ADB,△AEC,△BEC,△BDC,△ABC,△EBO,△DCO,共8个,
故选:A.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
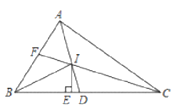
【题目】如图,在△ABC中,AD、CF分别是∠BAC、∠ACB的角平分线,且AD、CF交于点I, IE⊥B于E,下列结论:①∠BIE=∠CID;②S△ABC=![]() IE(AB+BC+AC);③BE=
IE(AB+BC+AC);③BE=![]() (AB+BC-AC);④AC=AF+DC.其中正确的结论是_______________ (填序号)
(AB+BC-AC);④AC=AF+DC.其中正确的结论是_______________ (填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
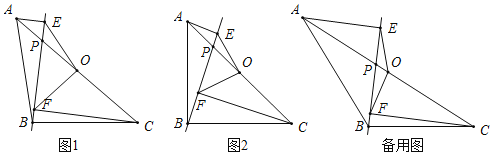
【题目】在△ABC中,AB=BC,点O是AC的中点,点P是AC上的一个动点(点P不与点A,O,C重合).过点A,点C作直线BP的垂线,垂足分别为点E和点F,连接OE,OF.
(1)如图1,请直接写出线段OE与OF的数量关系;
(2)如图2,当∠ABC=90°时,请判断线段OE与OF之间的数量关系和位置关系,并说明理由
(3)若|CF﹣AE|=2,EF=2![]() ,当△POF为等腰三角形时,请直接写出线段OP的长.
,当△POF为等腰三角形时,请直接写出线段OP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
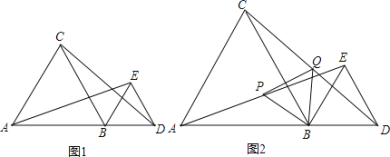
【题目】如图1,点B是线段AD上一点,△ABC和△BDE分别是等边三角形,连接AE和CD.
(1)求证:AE=CD;
(2)如图2,点P、Q分别是AE、CD的中点,试判断△PBQ的形状,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x与反比例函数y=![]() 的图象交于A,B两点,过点B作BD∥x轴,交y轴于点D,直线AD交反比例函数y=
的图象交于A,B两点,过点B作BD∥x轴,交y轴于点D,直线AD交反比例函数y=![]() 的图象于另一点C,则
的图象于另一点C,则![]() 的值为( )
的值为( )
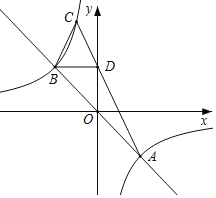
A. 1:3 B. 1:2![]() C. 2:7 D. 3:10
C. 2:7 D. 3:10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区一电瓶小客车接到任务从景区大门出发,向东走2千米到达A景区,继续向东走2.5千米到达B景区,然后又回头向西走8.5千米到达C景区,最后回到景区大门.
![]()
(1)以景区大门为原点,向东为正方向,以1个单位长表示1千米,建立如图所示的数轴,请在数轴上表示出上述A、B、C三个景区的位置.
(2)若电瓶车充足一次电能行走15千米,则该电瓶车能否在一开始充好电而途中不充电的情况下完成此次任务?请计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是( )

A. b2>4ac
B. ax2+bx+c≥﹣6
C. 若点(﹣2,m),(﹣5,n)在抛物线上,则m>n
D. 关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com