
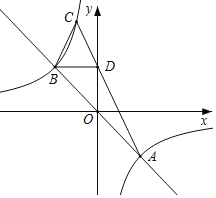
【题目】如图,直线y=﹣x与反比例函数y=![]() 的图象交于A,B两点,过点B作BD∥x轴,交y轴于点D,直线AD交反比例函数y=
的图象交于A,B两点,过点B作BD∥x轴,交y轴于点D,直线AD交反比例函数y=![]() 的图象于另一点C,则
的图象于另一点C,则![]() 的值为( )
的值为( )
A. 1:3 B. 1:2![]() C. 2:7 D. 3:10
C. 2:7 D. 3:10
【答案】A
【解析】联立直线AB与反比例函数解析式成方程组,通过解方程组可求出点A、B的坐标,由BD∥x轴可得出点D的坐标,由点A、D的坐标利用待定系数法可求出直线AD的解析式,联立直线AD与反比例函数解析式成方程组,通过解方程组可求出点C的坐标,再结合两点间的距离公式即可求出![]() 的值.
的值.
联立直线AB及反比例函数解析式成方程组,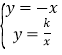 ,
,
解得: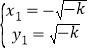 ,
,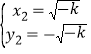 ,
,
∴点B的坐标为(﹣![]() ,
,![]() ),点A的坐标为(
),点A的坐标为(![]() ,﹣
,﹣![]() ),
),
∵BD∥x轴,
∴点D的坐标为(0,![]() ).
).
设直线AD的解析式为y=mx+n,
将A(![]() ,﹣
,﹣![]() )、D(0,
)、D(0,![]() )代入y=mx+n,
)代入y=mx+n,
![]() ,解得:
,解得:![]() ,
,
∴直线AD的解析式为y=﹣2+![]() ,
,
联立直线AD及反比例函数解析式成方程组,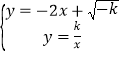 ,
,
解得: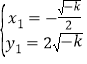 ,
,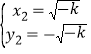 ,
,
∴点C的坐标为(﹣![]() ,2
,2![]() ).
).
∴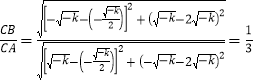 ,
,
故选A.


科目:初中数学 来源: 题型:
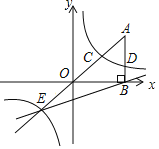
【题目】如图,在平面直角坐标系中,A点的坐标为(a,6),AB⊥x轴于点B,cos∠OAB═![]() ,反比例函数y=
,反比例函数y=![]() 的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为
的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为![]() .
.
(1)求反比例函数的解析式;
(2)求直线EB的解析式;
(3)求S△OEB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的解题过程,再解决问题.
解方程: x4 -6x2 +5=0.
这是一个一元四次方程,根据该方程的特点,它的通常解法是:
设 x2 = y ,则原方程可化为 y2 -6y+5=0.①
解这个方程,得 y1 =1, y2 =5.当 y =1时, x=±1;当 y=5时, x=±![]() .所以原方程有四个根: x1 =1, x2 =-1, x3 =
.所以原方程有四个根: x1 =1, x2 =-1, x3 =![]() , x4 =-
, x4 =-![]() .
.
(1)填空:在由原方程得到方程①的过程中,利用________法达到降次的目的,体现了________的数学思想.
(2)解方程:( x2 -x )2 -4(x2 -x )-12=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个二次函数的图象,三位同学分别说出了它的一些特点:
甲:对称轴为直线x=4
乙:与x轴两个交点的横坐标都是整数.
丙:与y轴交点的纵坐标也是整数,且以这三个点为顶点的三角形面积为3.请你写出满足上述全部特点的一个二次函数解析式__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k﹣1)x+k2+k﹣1=0有实数根.
(1)求k的取值范围;
(2)若此方程的两实数根x1,x2满足x12+x22=11,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )

A. 前2分钟,乙的平均速度比甲快
B. 5分钟时两人都跑了500米
C. 甲跑完800米的平均速度为100米/分
D. 甲乙两人8分钟各跑了800米
查看答案和解析>>
科目:初中数学 来源: 题型:
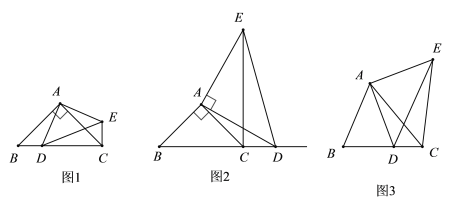
【题目】如图,在△ABC中,∠ABC为锐角,点D为直线BC上一动点,以AD为直角边且在AD的右侧作等腰直角三角形ADE,∠DAE=90°,AD=AE.
(1)如果AB=AC,∠BAC=90°.①当点D在线段BC上时,如图1,线段CE、BD的位置关系为___________,数量关系为___________
②当点D在线段BC的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.
(2)如图3,如果AB≠AC,∠BAC≠90°,点D在线段BC上运动。探究:当∠ACB多少度时,CE⊥BC?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com