
【题目】已知关于x的一元二次方程x2﹣(2k﹣1)x+k2+k﹣1=0有实数根.
(1)求k的取值范围;
(2)若此方程的两实数根x1,x2满足x12+x22=11,求k的值.
【答案】(1)k≤![]() ;(2)k=﹣1.
;(2)k=﹣1.
【解析】
(1)根据方程有实数根得出△=[﹣(2k﹣1)]2﹣4×1×(k2+k﹣1)=﹣8k+5≥0,解之可得;
(2)利用根与系数的关系可用k表示出x1+x2和x1x2的值,根据条件可得到关于k的方程,可求得k的值,注意利用根的判别式进行取舍.
(1)∵关于x的一元二次方程x2﹣(2k﹣1)x+k2+k﹣1=0有实数根,
∴△≥0,即[﹣(2k﹣1)]2﹣4×1×(k2+k﹣1)=﹣8k+5≥0,
解得k≤![]() ;
;
(2)由根与系数的关系可得x1+x2=2k﹣1,x1x2=k2+k﹣1,
∴x12+x22=(x1+x2)2﹣2x1x2=(2k﹣1)2﹣2(k2+k﹣1)=2k2﹣6k+3,
∵x12+x22=11,
∴2k2﹣6k+3=11,解得k=4,或k=﹣1,
∵k≤![]() ,
,
∴k=4(舍去),
∴k=﹣1.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】“十一”黄金周期间,各地景区游人如织,其中淮安动物园在9月30日的游客人数为1万人,接下来的七天假期中每天接待的游客人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数).
日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
人数变化 (单位:万人) |
|
|
|
|
|
|
|
(1)请根据计算判断七天内游客人数最多的是哪天,有多少万人?
(2)若以9月30日的游客人数1万人为标准,每人门票均为10元,问黄金周期间淮安动物园平均每天门票多收入多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 、
、![]() 在数轴上,
在数轴上,![]() 对应的数是
对应的数是![]() ,点
,点![]() 在
在![]() 的右边,且距
的右边,且距![]() 点4个单位长度,点
点4个单位长度,点![]() 、
、![]() 是数轴上两个动点;
是数轴上两个动点;
(1)点![]() 所对应的数为 ;
所对应的数为 ;
(2)当点![]() 到点
到点![]() 、
、![]() 的距离之和是5个单位时,点
的距离之和是5个单位时,点![]() 所对应的数是多少?
所对应的数是多少?
(3)如果![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 出发,均沿数轴向左运动,点
出发,均沿数轴向左运动,点![]() 每秒走2个单位长度,先出发5秒钟,点
每秒走2个单位长度,先出发5秒钟,点![]() 每秒走3个单位长度,当
每秒走3个单位长度,当![]() 、
、![]() 两点相距2个单位长度时,点
两点相距2个单位长度时,点![]() 、
、![]() 对应的数各是多少?
对应的数各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
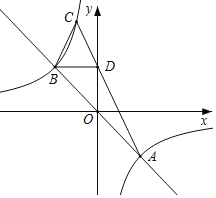
【题目】如图,直线y=﹣x与反比例函数y=![]() 的图象交于A,B两点,过点B作BD∥x轴,交y轴于点D,直线AD交反比例函数y=
的图象交于A,B两点,过点B作BD∥x轴,交y轴于点D,直线AD交反比例函数y=![]() 的图象于另一点C,则
的图象于另一点C,则![]() 的值为( )
的值为( )
A. 1:3 B. 1:2![]() C. 2:7 D. 3:10
C. 2:7 D. 3:10
查看答案和解析>>
科目:初中数学 来源: 题型:
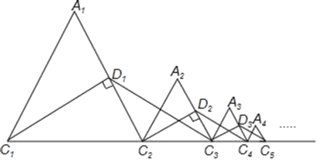
【题目】如图,等边△A1C1C2的周长为1,作C1D1⊥A1C2于D1,在C1C2的延长线上取点C3,使D1C3=D1C1,连接D1C3,以C2C3为边作等边△A2C2C3;作C2D2⊥A2C3于D2,在C2C3的延长线上取点C4,使D2C4=D2C2,连接D2C4,以C3C4为边作等边△A3C3C4;…且点A1,A2,A3,…都在直线C1C2同侧,如此下去,则△A1C1C2,△A2C2C3,△A3C3C4,…,△AnnCn+1的周长和为_____.(n≥2,且n为整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
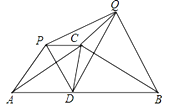
【题目】如图,等腰△ABC中,CA=CB=6,∠ACB=120°,点D在线段AB上运动(不与A、B重合),将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,给出下列结论:
①CD=CP=CQ;②∠PCQ为定值;③△PCQ面积的最小值为![]() ;④当点D在AB的中点时,△PDQ是等边三角形,其中正确结论的个数为( )
;④当点D在AB的中点时,△PDQ是等边三角形,其中正确结论的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 没有实数根,甲由于看错了二次项系数,求得两个根为3和6,乙由于看错了某一项系数的符号,求得两个根为
没有实数根,甲由于看错了二次项系数,求得两个根为3和6,乙由于看错了某一项系数的符号,求得两个根为![]() 和
和![]() ,则
,则![]() =____________
=____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠B=∠C,∠ADB=∠DEC,AB=DC.
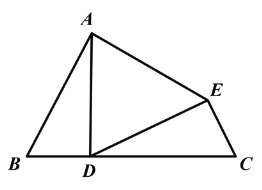
(1)求证:△ADE 为等腰三角形.
(2)若∠B=60°,求证:△ADE 为等边三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com