练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，点在等边的边上，，射线于点，点是射线上一动点，点是线段上一动点，当的值最小时，，则为( )

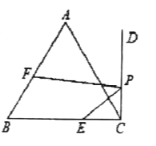
    A. 14B. 13C. 12D. 10

    【答案】D

    【解析】

    根据等边三角形的性质得到AC=BC，∠B=60°，作点E关于直线CD的对称点G，过G作GF⊥AB于F，交CD于P，则此时，EP+PF的值最小，根据直角三角形的性质得到BG=2BF=14，求得EG=8，于是得到结论．

    解：∵△ABC是等边三角形，

    ∴AC=BC，∠B=60°，

    作点E关于直线CD的对称点G，过G作GF⊥AB于F，交CD于P，

    则此时，EP+PF的值最小，

    ∵∠B=60°，∠BFG=90°，

    ∴∠G=30°，

    ∵BF=7，

    ∴BG=2BF=14，

    ∴EG=8，

    ∵CE=CG=4，

    ∴AC=BC=10，

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠MON=90，A是∠MON内部的一点，过点A作AB⊥ON，垂点为点B，AB=3厘米，OB=4厘米，动点E、F同时从O点出发，点E以1.5厘米/秒的速度沿ON方向运动，点F以2厘米/秒的速度沿OM方向运动，EF与OA交于点C，连接AE，当点E到达点B时，点F随之停止运动。设运动时间为t秒（t＞0）。

    （1）当t=1秒时，ΔEOF与ΔABO是否相似？请说明理由。

    （2）在运动过程中，不论t取何值时，总有EF⊥OA，为什么？

    （3）连接AF，在运动过程中，是否存在某一时刻t，使得SΔAEF=S四边形ABOF ？若存在，请求出此时t的值；若不存在，请说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先阅读下面的解题过程,再解决问题.

    解方程: x4 －6x2 +5=0.

    这是一个一元四次方程,根据该方程的特点,它的通常解法是:

    设 x2 = y ,则原方程可化为 y2 －6y+5=0.①

    解这个方程,得 y1 =1, y2 =5.当 y =1时, x=±1;当 y=5时, x=±.所以原方程有四个根: x1 =1, x2 =－1, x3 =, x4 =－.

    （1）填空:在由原方程得到方程①的过程中,利用________法达到降次的目的,体现了________的数学思想.

    （2）解方程:（ x2 －x ）2 －4（x2 －x ）－12=0.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，∠A=36°，BD，CE是角平分线，则图中的等腰三角形共有

    A. 8个 B. 7个 C. 6个 D. 5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的一元二次方程x2﹣（2k﹣1）x+k2+k﹣1=0有实数根．

    （1）求k的取值范围；

    （2）若此方程的两实数根x1，x2满足x12+x22=11，求k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y=x2+bx+c经过点A（﹣2，0），B（0、﹣4）与x轴交于另一点C，连接BC．

    （1）求抛物线的解析式；

    （2）如图，P是第一象限内抛物线上一点，且S△PBO=S△PBC，求证：AP∥BC；

    （3）在抛物线上是否存在点D，直线BD交x轴于点E，使△ABE与以A，B，C，E中的三点为顶点的三角形相似（不重合）？若存在，请求出点D的坐标；若不存在，请说明理由．

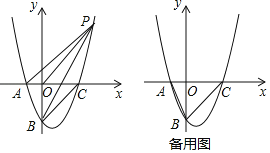
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两人进行慢跑练习，慢跑路程y（米）与所用时间t（分钟）之间的关系如图所示，下列说法错误的是（ ）

    A. 前2分钟，乙的平均速度比甲快

    B. 5分钟时两人都跑了500米

    C. 甲跑完800米的平均速度为100米/分

    D. 甲乙两人8分钟各跑了800米

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在菱形ABCD中，点P是BC边上一动点，连结AP，AP的垂直平分线交BD于点G，交 AP于点E，在P点由B点到C点的运动过程中，∠APG的大小变化情况是( )

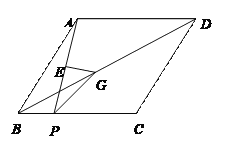
    A. 变大 B. 先变大后变小 C. 先变小后变大 D. 不变

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y＝ax2＋bx－5(a≠0)经过点A(4，－5)，与x轴的负半轴交于点B，与y轴交于点C，且OC＝5OB，抛物线的顶点为点D.

    (1)求这条抛物线的表达式；

    (2)连接AB、BC、CD、DA，求四边形ABCD的面积．

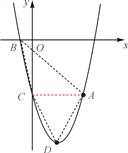
    查看答案和解析>>

    同步练习册答案