
【题目】如图,等腰△ABC中,CA=CB=6,∠ACB=120°,点D在线段AB上运动(不与A、B重合),将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,给出下列结论:
①CD=CP=CQ;②∠PCQ为定值;③△PCQ面积的最小值为![]() ;④当点D在AB的中点时,△PDQ是等边三角形,其中正确结论的个数为( )
;④当点D在AB的中点时,△PDQ是等边三角形,其中正确结论的个数为( )
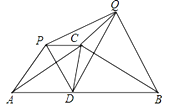
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】①由折叠直接得到结论;②由折叠的性质求出∠ACP +∠BCQ=120°,再用周角的定义求出∠PCQ=120°;③先作出△PCQ的边PC上的高,用三角函数求出QE=![]() CQ,得到S△PCQ =
CQ,得到S△PCQ =![]() CD2,判断出△PCQ面积最小时,点D的位置,再求△PCQ面积的最小值即可;④先判断出△APD 是等边三角形,△BDQ是等边三角形,再求出∠PDQ=60°,即可得结论.
CD2,判断出△PCQ面积最小时,点D的位置,再求△PCQ面积的最小值即可;④先判断出△APD 是等边三角形,△BDQ是等边三角形,再求出∠PDQ=60°,即可得结论.
① ∵将△ CAD 与△ CBD 分别沿直线 CA、CB 翻折得到△CAP与△CBQ ,
∴CP=CD=CQ,
∴ ①正确;
② ∵将△ CAD与△CBD 分别沿直线CA、CB翻折得到△CAP 与△CBQ ,
∴∠ACP=∠ACD,∠BCQ=∠BCD ,
∴∠ACP +∠BCQ=∠ACD +∠BCD=∠ACB=120°,
∴∠ PCQ=360°﹣(∠ACP +BCQ +∠ACB ) =360°﹣(120°+120°) =120°,
∴∠ PCQ 的大小不变;
∴ ② 正确;
③ 如图,过点Q作QE ⊥ PC 交PC延长线于 E ,

∵∠PCQ=120°,
∴∠QCE=60°,
在 Rt△QCE 中, sin∠QCE=![]() ,
,
∴QE=CQ×sin∠QCE=CQ×sin60°=![]() CQ ,
CQ ,
∵CP=CD=CQ,
∴ S△PCQ =![]() ×CP×QE=
×CP×QE=![]() CP×CQ=
CP×CQ=![]() CD 2,
CD 2,
∴ CD 最短时,S △ PCQ最小,
即:CD ⊥ AB 时,CD最短,
过点 C 作 CF ⊥ AB,此时 CF 就是最短的 CD ,
∵ AC=BC=6,∠ ACB=120°,
∴∠ ABC=30°,
∴CF=![]() BC=3,
BC=3,
即:CD最短为3,
∴ S △ PCQ最小 =![]() ,
,
∴ ③错误;
④ ∵将△CAD与△CBD 分别沿直线CA、CB翻折得到△CAP与△CBQ ,
∴ AD=AP,∠ DAC=∠ PAC,
∵∠ DAC=30°,
∴∠ APD=60°,
∴△ APD是等边三角形,
∴ PD=AD,∠ ADP=60°,
同理:△ BDQ是等边三角形,
∴ DQ=BD,∠ BDQ=60°,
∴∠ PDQ=60°,
∵当点D在AB的中点,
∴AD=BD,
∴PD=DQ,
∴△DPQ 是等边三角形.
∴ ④正确.
正确的答案为:①②④ .
故选C.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
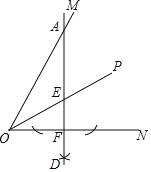
【题目】如图,OP平分∠MON,A是边OM上一点,以点A为圆心、大于点A到ON的距离为半径作弧,交ON于点B、C,再分别以点B、C为圆心,大于![]() BC的长为半径作弧,两弧交于点D、作直线AD分别交OP、ON于点E、F.若∠MON=60°,EF=1,则OA=__.
BC的长为半径作弧,两弧交于点D、作直线AD分别交OP、ON于点E、F.若∠MON=60°,EF=1,则OA=__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个二次函数的图象,三位同学分别说出了它的一些特点:
甲:对称轴为直线x=4
乙:与x轴两个交点的横坐标都是整数.
丙:与y轴交点的纵坐标也是整数,且以这三个点为顶点的三角形面积为3.请你写出满足上述全部特点的一个二次函数解析式__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k﹣1)x+k2+k﹣1=0有实数根.
(1)求k的取值范围;
(2)若此方程的两实数根x1,x2满足x12+x22=11,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】班级组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动,基地离学校有90公里,队伍8:00从学校出发.苏老师因有事情,8:30从学校自驾小车以大巴1.5倍的速度追赶,追上大巴后继续前行,结果比队伍提前15分钟到达基地.问:
(1)大巴与小车的平均速度各是多少?
(2)苏老师追上大巴的地点到基地的路程有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )

A. 前2分钟,乙的平均速度比甲快
B. 5分钟时两人都跑了500米
C. 甲跑完800米的平均速度为100米/分
D. 甲乙两人8分钟各跑了800米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图象,根据图象回答下列问题:

(1)当行使8千米时,收费应为 元;
(2)从图象上你能获得哪些信息?(请写出2条)
① ________
②____________________________
(3)求出收费y(元)与行使x(千米)(x≥3)之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次科技知识竞赛中,两组学生成绩统计如下表,通过计算可知两组的方差为![]() ,
, ![]() .下列说法:
.下列说法:
①两组的平均数相同;
②甲组学生成绩比乙组学生成绩稳定;
③甲组成绩的众数>乙组成绩的众数;
④两组成绩的中位数均为80,但成绩≥80的人数甲组比乙组多,从中位数来看,甲组成绩总体比乙组好;⑤成绩高于或等于90分的人数乙组比甲组多,高分段乙组成绩比甲组好.其中正确的共有( )
分数 | 50 | 60 | 70 | 80 | 90 | 100 | |
人 | 甲组 | 2 | 5 | 10 | 13 | 14 | 6 |
乙组 | 4 | 4 | 16 | 2 | 12 | 12 | |
A. 2种 B. 3种 C. 4种 D. 5种
查看答案和解析>>
科目:初中数学 来源: 题型:
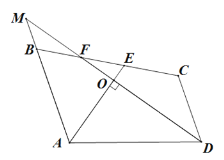
【题目】如图,四边形 ABCD 中,AE,DF 分别是∠BAD,∠ADC 的平分线,且 AE⊥DF 于点 O . 延长 DF 交 AB 的延长线于点 M .
(1)求证:AB∥DC ;
(2)若∠MBC=120°,∠BAD=108°,求∠C,∠DFE 的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com