
【题目】已知![]() 、
、![]() 在数轴上,
在数轴上,![]() 对应的数是
对应的数是![]() ,点
,点![]() 在
在![]() 的右边,且距
的右边,且距![]() 点4个单位长度,点
点4个单位长度,点![]() 、
、![]() 是数轴上两个动点;
是数轴上两个动点;
(1)点![]() 所对应的数为 ;
所对应的数为 ;
(2)当点![]() 到点
到点![]() 、
、![]() 的距离之和是5个单位时,点
的距离之和是5个单位时,点![]() 所对应的数是多少?
所对应的数是多少?
(3)如果![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 出发,均沿数轴向左运动,点
出发,均沿数轴向左运动,点![]() 每秒走2个单位长度,先出发5秒钟,点
每秒走2个单位长度,先出发5秒钟,点![]() 每秒走3个单位长度,当
每秒走3个单位长度,当![]() 、
、![]() 两点相距2个单位长度时,点
两点相距2个单位长度时,点![]() 、
、![]() 对应的数各是多少?
对应的数各是多少?
【答案】(1)1;(2)![]() 或
或![]() ;(3)
;(3)![]() ,
,![]() 或
或![]() ,
,![]()
【解析】
(1)根据两点间的距离公式即可求解;
(2)设P点对应的数为![]() ,分①点P在点M的左边,②点P在点N的右边两种情况进行讨论即可求解;
,分①点P在点M的左边,②点P在点N的右边两种情况进行讨论即可求解;
(3)设点Q运动t秒时,P、Q两点相距2个单位长度,依题意得关于t的绝对值方程,求解即可.
(1)![]() .
.
故点N所对应的数是1;
(2)设P点对应的数为![]() ,
,
依题意得:![]()
①当点P在点M的左边,即![]() 时,
时,
![]() ,
,
解得:![]() ,
,
②当点P在点N的右边,即![]() 时,
时,
![]() ,
,
解得:![]() ;
;
故点P所对应的数是:![]() 或
或![]() ;
;
(3)设点Q运动t秒时,P、Q两点相距2个单位长度,
此时点P所对应的数是![]() ,
,
点Q所对应的数是![]() ,
,
依题意得:![]() ,
,
整理得:![]() ,
,
解得:![]() 或
或![]() ,
,
当![]() 时,
时,
点P对应的数是![]() ,点Q对应的数是
,点Q对应的数是![]() ,
,
当![]() 时,
时,
点P对应的数是![]() ,点Q对应的数是
,点Q对应的数是![]() .
.
故点P、点Q对应的数分别是![]() ,
,![]() 或
或![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】在等边三角形![]() 中
中![]() 点
点![]() 是
是![]() 边上的一点,点
边上的一点,点![]() 是
是![]() 边上的一点,连接
边上的一点,连接![]() 以
以![]() 为边作等边三角形
为边作等边三角形![]() 连接
连接![]() .
.
![]() 如图1,当点
如图1,当点![]() 与点
与点![]() 重合时,
重合时,
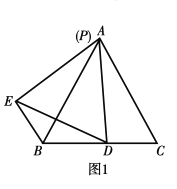
![]() 找出图中的一对全等三角形,并证明;
找出图中的一对全等三角形,并证明;
![]() ;
;
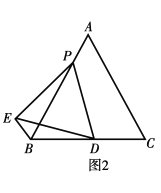
![]() 如图2,若
如图2,若![]() 请计算
请计算![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
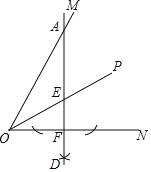
【题目】如图,OP平分∠MON,A是边OM上一点,以点A为圆心、大于点A到ON的距离为半径作弧,交ON于点B、C,再分别以点B、C为圆心,大于![]() BC的长为半径作弧,两弧交于点D、作直线AD分别交OP、ON于点E、F.若∠MON=60°,EF=1,则OA=__.
BC的长为半径作弧,两弧交于点D、作直线AD分别交OP、ON于点E、F.若∠MON=60°,EF=1,则OA=__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入它所在的数集的括号里.
﹣![]() ,+5,﹣6.3,0,﹣
,+5,﹣6.3,0,﹣![]() ,2
,2![]() ,6.9,﹣7,210,0.031,﹣43,﹣10%
,6.9,﹣7,210,0.031,﹣43,﹣10%
正数集合:{ …}
整数集合:{ …}
非负数集合:{ …}
负分数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的解题过程,再解决问题.
解方程: x4 -6x2 +5=0.
这是一个一元四次方程,根据该方程的特点,它的通常解法是:
设 x2 = y ,则原方程可化为 y2 -6y+5=0.①
解这个方程,得 y1 =1, y2 =5.当 y =1时, x=±1;当 y=5时, x=±![]() .所以原方程有四个根: x1 =1, x2 =-1, x3 =
.所以原方程有四个根: x1 =1, x2 =-1, x3 =![]() , x4 =-
, x4 =-![]() .
.
(1)填空:在由原方程得到方程①的过程中,利用________法达到降次的目的,体现了________的数学思想.
(2)解方程:( x2 -x )2 -4(x2 -x )-12=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个二次函数的图象,三位同学分别说出了它的一些特点:
甲:对称轴为直线x=4
乙:与x轴两个交点的横坐标都是整数.
丙:与y轴交点的纵坐标也是整数,且以这三个点为顶点的三角形面积为3.请你写出满足上述全部特点的一个二次函数解析式__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k﹣1)x+k2+k﹣1=0有实数根.
(1)求k的取值范围;
(2)若此方程的两实数根x1,x2满足x12+x22=11,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次科技知识竞赛中,两组学生成绩统计如下表,通过计算可知两组的方差为![]() ,
, ![]() .下列说法:
.下列说法:
①两组的平均数相同;
②甲组学生成绩比乙组学生成绩稳定;
③甲组成绩的众数>乙组成绩的众数;
④两组成绩的中位数均为80,但成绩≥80的人数甲组比乙组多,从中位数来看,甲组成绩总体比乙组好;⑤成绩高于或等于90分的人数乙组比甲组多,高分段乙组成绩比甲组好.其中正确的共有( )
分数 | 50 | 60 | 70 | 80 | 90 | 100 | |
人 | 甲组 | 2 | 5 | 10 | 13 | 14 | 6 |
乙组 | 4 | 4 | 16 | 2 | 12 | 12 | |
A. 2种 B. 3种 C. 4种 D. 5种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com