
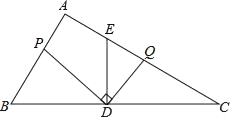
【题目】如图,在Rt△ABC中,∠A=90°,AB=12,AC=16,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上的一动点,点Q为边AC上的一动点,且∠PDQ=90°.
(1)求ED、EC的长;
(2)若BP=2,求CQ的长;
(3)若线段PQ与线段DE的交点为F,当△PDF为等腰三角形时,求BP的长.
【答案】(1)DE=![]() ,CE=
,CE=![]() ;(2)CQ的长为11或14;(3)BP=
;(2)CQ的长为11或14;(3)BP=![]() 或
或![]() .
.
【解析】(1)先根据勾股定理求得BC的长,再结合点D为BC的中点可得CD的长,然后证得△ABC∽△DEC,根据相似三角形的性质即可求得结果;(2)分点P在AB边上和点P在AB的延长线上两种情况求解即可;(3)先证得△PDF∽△CDQ,因△PDF为等腰三角形 可得△CDQ为等腰三角形,再分CQ=CD、QC=QD和DC=DQ三种情况,根据等腰三角形的性质求解即可.
(1)∵∠A=90°,AB=12,AC=16,
∴根据勾股定理得到,BC=![]() =20,
=20,
∴CD=![]() BC=10,
BC=10,
∵DE⊥BC,
∴∠A=∠CDE=90°,∠C=∠C,
∴△CDE∽△CAB,
∴DE:AB=CE:CB=CD:CA,
即DE:12=CE:20=10:16,
∴DE=![]() ,CE=
,CE=![]() ;
;
(2)分两种情况考虑:
如图,∵△CDE∽△CAB,
∴∠B=∠DEC,
∵∠PDQ=90°,
∴∠QDC+∠PDB=90°,
∵∠QDC+∠EDQ=90°,
∴∠EDQ=∠PDB,
∴△PBD∽△QED,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴EQ=![]() ,
,
∴CQ=CE﹣EQ=![]() ﹣
﹣![]() =11;
=11;
如图2,
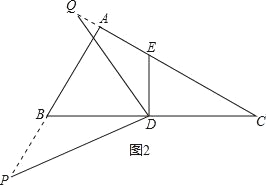
∵∠B=DEC,
∴∠PBD=∠QED,
∵∠PDQ=90°
∴∠BPD+∠QDB=90°,
∵∠QDE+∠QDB=90°,
∴∠BDP=∠QDE,
∴△PBD∽△QED,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴EQ=![]() ,
,
∴CQ=![]() +
+![]() =14,
=14,
则CQ的长为11或14;
(3)∵线段PQ与线段DE的交点为点FF,
∴点P在边AB上,
∵△BPD∽△EQD,
∴![]() =
=![]() =
=![]() =
=![]() =
=![]() ,
,
若设BP=x,则EQ=![]() x,CQ=
x,CQ=![]() ﹣
﹣![]() x,
x,
∵cot∠QPD=![]() =
=![]() ,cotC=
,cotC=![]() =
=![]() =
=![]() ,
,
∴∠QPD=∠C,
∵∠PDE=∠CDQ,∴△PDF∽△CDQ,
∵△PDF为等腰三角形,
∴△CDQ为等腰三角形,
①当CQ=CD时,可得:![]() ﹣
﹣![]() x=10,
x=10,
解得:x=![]() ;
;
②当QC=QD时,过点Q作QM⊥CB于M,如图3所示,

∴CM=![]() CD=5,
CD=5,
∵cos∠C=![]() =
=![]() =
=![]() =
=![]() ,
,
∴CQ=![]() ,
,
∴![]() ﹣
﹣![]() x=
x=![]() ,
,
解得:x=![]() ;
;
③当DC=DQ时,过点D作DN⊥CQ于N,如图4所示,
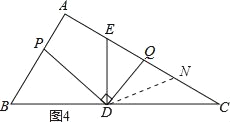
∴CQ=2CN,
∵cos∠C=![]() =
=![]() =
=![]() ,
,
∴CN=8,
∴CQ=16,
∴![]() ﹣
﹣![]() x=16,
x=16,
解得:x=﹣![]() (舍去),
(舍去),
∴综上所述,BP=![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】阅读理解:
若![]() ,
,![]() ,
,![]() 为数轴上三点且点
为数轴上三点且点![]() 在
在![]() ,
,![]() 之间,若点
之间,若点![]() 到
到![]() 的距离是点
的距离是点![]() 到
到![]() 的距离的3倍,我们就称点
的距离的3倍,我们就称点![]() 是
是![]() 的好点.
的好点.
如图1,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为2.表示1的点
表示的数为2.表示1的点![]() 到
到![]() 的距离是3,到
的距离是3,到![]() 的距离是1,那么点
的距离是1,那么点![]() 是
是![]() 的好点;又如,表示
的好点;又如,表示![]() 的点
的点![]() 到
到![]() 的距离是1,到
的距离是1,到![]() 的距离是3,那么点
的距离是3,那么点![]() 就不是
就不是![]() 的好点,但点
的好点,但点![]() 是
是![]() 的好点.
的好点.
知识运用:
(1)若![]() 、
、![]() 为数轴上两点,点
为数轴上两点,点![]() 所表示的数为
所表示的数为![]() ,点
,点![]() 所表示的数为2.
所表示的数为2.
数 所表示的点是![]() 的好点;
的好点;
数 所表示的点是![]() 的好点;
的好点;
(2)若点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 在点
在点![]() 的右边,且点
的右边,且点![]() 在
在![]() ,
,![]() 之间,点
之间,点![]() 是
是![]() 的好点,求点
的好点,求点![]() 所表示的数(用含
所表示的数(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
(3)若![]() 、
、![]() 为数轴上两点,点
为数轴上两点,点![]() 所表示的数为
所表示的数为![]() ,点
,点![]() 所表示的数为27,现有一只电子蚂蚁
所表示的数为27,现有一只电子蚂蚁![]() 从点
从点![]() 出发,以每秒6个单位的速度向右运动,运动时间为
出发,以每秒6个单位的速度向右运动,运动时间为![]() 秒.如果
秒.如果![]() ,
,![]() ,
,![]() 中恰有一个点为其余两点的好点,求
中恰有一个点为其余两点的好点,求![]() 的值.
的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21.动点P从点D出发,沿射线DA的方向以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).当t为__________ 时,以B,P,Q三点为顶点的三角形是等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
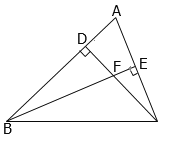
【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,AC的垂直平分线BE与CD交于点F,与AC交于点E.
(1)判断△DBC的形状并证明你的结论.
(2)求证:BF=AC.
(3)试说明CE=![]() BF.
BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2﹣4x+c经过点A(2,0).
(1)求抛物线的解析式和顶点坐标;
(2)若点B(m,n)是抛物线上的一动点,点B关于原点的对称点为C.
①若B、C都在抛物线上,求m的值;
②若点C在第四象限,当AC2的值最小时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
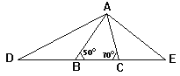
【题目】如图,若△ABC的∠ABC=50°,∠ACB=70°,延长CB至点D,使BD=BA,延长BC至E点,使CE=CA, 连接AD、AE,则∠DAE的度数为__________度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,O是AC、BD的交点,过点O 与AC垂直的直线交边AD于点E,若□ABCD的周长为22cm,则△CDE的周长为( ).
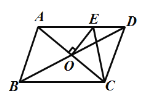
A. 8cm B. 10cm C. 11cm D. 12cm
查看答案和解析>>
科目:初中数学 来源: 题型:
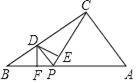
【题目】如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点P在边AB上,∠CPB的平分线交边BC于点D,DE⊥CP于点E,DF⊥AB于点F.当△PED与△BFD的面积相等时,BP的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
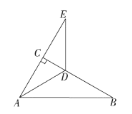
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,试说明DA=DE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com