练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

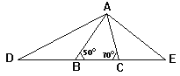
    【题目】如图,若△ABC的∠ABC＝50°,∠ACB＝70°，延长CB至点D,使BD＝BA,延长BC至E点,使CE＝CA, 连接AD、AE,则∠DAE的度数为__________度.

    【答案】120

    【解析】

    由题意知△ABD和△ACE均为等腰三角形，可由三角形内角和定理求得∠BAC的度数，用三角形外角的性质求得∠DAB与∠CAE的度数，即可求得∠DAE的度数．

    解：∵∠ABC＝50°，∠ACB＝70°，

    ∴∠BAC＝180°∠ABC∠ACB＝180°50°70°＝60°，

    ∵BD＝BA，

    ∴∠D＝∠DAB＝∠ABC＝25°，

    ∵CE＝CA，

    ∴∠E＝∠CAE＝∠ACB＝35°，

    ∴∠DAE＝∠DAB＋∠BAC＋∠CAE＝25°＋60°＋35°＝120°，

    故答案为：120.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】2020年高峡水库蓄水达到了177米的设计目标水位.据测算，蓄水达到177米目标水位后，高峡水库电站的年发电量将达到842.4亿千瓦时，比2017年要多发电20%.据资料显示，火力发电时每燃烧12吨标准原煤可发电2.5万千瓦时.（千瓦时为一种能量单位）

    （1）求2017年高峡电站的年发电量；

    （2）请计算高峡电站2020年全年发电量与2017年全年发电量相比，可为国家多节约标准原煤多少万吨？

    （3）已知2019年全年发电量比2018年增加了10%，2018年与2019年的发电量之和比2017年发电量的2倍还多129亿千瓦时，求2018年和2019年高峡电站年发电量．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线a，b，c表示交叉的三条公路，现要建一货物中转站，要求它到这三条公路的距离相等，则可供选择的站址最多有　　

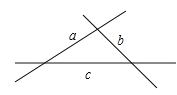
    A. 4个B. 3个C. 2个D. 1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

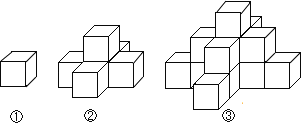
    【题目】如图①是一个水平放置的小正方体木块，图②、图③是由这样的小正方体木块叠放而成，按照这样的规律继续叠放下去，第四个叠放的图形时，小正方体木块总数应是___块；第七个叠放的图形时，小正方体木块总数应是____块．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

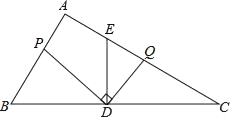
    【题目】如图，在Rt△ABC中，∠A=90°，AB=12，AC=16，点D为边BC的中点，DE⊥BC交边AC于点E，点P为射线AB上的一动点，点Q为边AC上的一动点，且∠PDQ=90°．

    （1）求ED、EC的长；

    （2）若BP=2，求CQ的长；

    （3）若线段PQ与线段DE的交点为F，当△PDF为等腰三角形时，求BP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图 ，等腰三角形PEF中，PE=PF，点O在EF边上（异于点E，F），点Q是PO延长线上一点，若△EFQ为等腰三角形，则称点Q为△PEF的“同类点”.

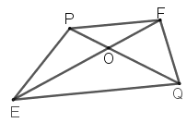
    （1）如图，BG平分∠MBN，过射线BM上的点A作AD∥BN，交射线BG于点D，点O为BD上一点，连接AO并延长交射线BN于点C，若∠BAD=100°，∠BCD=70°，求证：点C是△ABD的“同类点”；

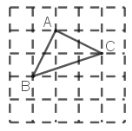
    （2）如图③，在5×5的正方形网格图上有一个△ABC，点A，B，C均在格点上，在给出的网格图上有一个格点D，使得点D为△ABC的“同类点”，则这样的点D共有__________个；

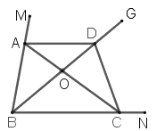
    （3）凸四边形ABCD中，∠ABC=110°，DA=AB=BC，对角线AC，BD交于点O，且BD≠CD，若点C为△ABD的“同类点”，请直接写出满足条件的∠ADC的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料：

    小明遇到这样一个问题：

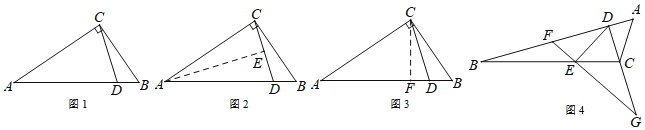
    如图1，△ABC中，∠ACB=90°，点D在AB上，且∠BAC=2∠DCB，求证：AC=AD．

    小明发现，除了直接用角度计算的方法外，还可以用下面两种方法：

    方法1：如图2，作AE平分∠CAB，与CD相交于点E．

    方法2：如图3，作∠DCF=∠DCB，与AB相交于点F．

    （1）根据阅读材料，任选一种方法，证明AC=AD．

    用学过的知识或参考小明的方法，解决下面的问题：

    （2）如图4，△ABC中，点D在AB上，点E在BC上，且∠BDE=2∠ABC，点F在BD上，且∠AFE=∠BAC，延长DC、FE，相交于点G，且∠DGF=∠BDE．

    ①在图中找出与∠DEF相等的角，并加以证明；

    ②若AB=kDF，猜想线段DE与DB的数量关系，并证明你的猜想．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校为了预测本校九年级男生毕业体育测试达标情况，随机抽取该年级部分男生进行了一次测试（满分50分，成绩均记为整数分），并按测试成绩m（单位：分）分成四类：A类（45＜m≤50），B类（40＜m≤45），C类（35＜m≤40），D类（m≤35）绘制出如图所示的两幅不完整的统计图，请根据图中信息解答下列问题：

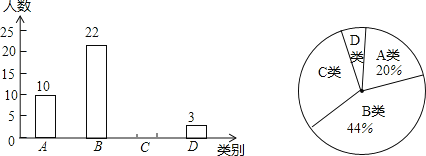
    （1）求本次抽取的样本容量和扇形统计图中A类所对的圆心角的度数；

    （2）若该校九年级男生有500名，D类为测试成绩不达标，请估计该校九年级男生毕业体育测试成绩能达标的有多少名？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知BD是△ABC的角平分线，CD是△ABC的外角∠ACE的外角平分线，CD与BD交于点D．

    （1）若∠A=50°，则∠D=　 　；

    （2）若∠A=80°，则∠D=　 　；

    （3）若∠A=130°，则∠D=　 　；

    （4）若∠D=36°，则∠A=　 　；

    （5）综上所述，你会得到什么结论？证明你的结论的准确性．

    查看答案和解析>>

    同步练习册答案