
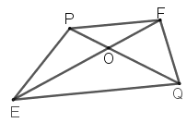
【题目】如图 ,等腰三角形PEF中,PE=PF,点O在EF边上(异于点E,F),点Q是PO延长线上一点,若△EFQ为等腰三角形,则称点Q为△PEF的“同类点”.
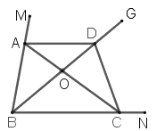
(1)如图,BG平分∠MBN,过射线BM上的点A作AD∥BN,交射线BG于点D,点O为BD上一点,连接AO并延长交射线BN于点C,若∠BAD=100°,∠BCD=70°,求证:点C是△ABD的“同类点”;
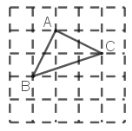
(2)如图③,在5×5的正方形网格图上有一个△ABC,点A,B,C均在格点上,在给出的网格图上有一个格点D,使得点D为△ABC的“同类点”,则这样的点D共有__________个;
(3)凸四边形ABCD中,∠ABC=110°,DA=AB=BC,对角线AC,BD交于点O,且BD≠CD,若点C为△ABD的“同类点”,请直接写出满足条件的∠ADC的度数.
【答案】(1)见解析;(2)4;(3)∠ADC的度数为125°或110°.
【解析】
(1)根据平行线的性质和角平分线的性质可得△ABD是等腰三角形,然后可求出∠ABD=∠ADB=∠DBC=40°,利用三角形内角和定理求出∠BDC的度数即可得到△BCD为等腰三角形,即点C是△ABD的“同类点”;
(2)找出所有在BC下方能使△BCD为等腰三角形的格点D即可;
(3)根据点C为△ABD的“同类点”可知△BCD为等腰三角形,然后分情况讨论:①当BD=BC时,②当BC=CD时,分别作出图形,根据等边三角形的判定和性质以及等腰三角形的性质求解即可.
解:(1)∵BG平分∠MBN,
∴∠ABD=∠DBC,
∵AD∥BN,
∴∠ADB=∠DBC,
∴∠ADB=∠ABD,
∴△ABD是等腰三角形,
又∵∠BAD=100°,
∴∠ABD=∠ADB=∠DBC=40°,
∵∠BCD=70°,
∴∠BDC=180°-∠DBC-∠BCD=180°-40°-70°=70°,
∴△BCD为等腰三角形,
∴点C是△ABD的“同类点”;
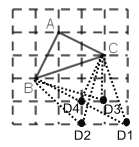
(2)如图所示:这样的点D共有4个;
(3)∵∠ABC=110°,DA=AB=BC,BD≠CD,点C为△ABD的“同类点”,
分情况讨论:
①如图,当BD=BC时,则BD=BC=DA=AB,
∴△ABD是等边三角形,
∴∠ABD=∠ADB=60°,
∴∠DBC=110°-60°=50°,
∴∠BDC=![]() ,
,
∴∠ADC=∠ADB+∠BDC=60°+65°=125°;

②如图,当BC=CD时,
则∠ABD=∠ADB,∠CDB=∠CBD,
∴∠ADB+∠CDB=∠ABD+∠CBD,
∴∠ADC=∠ABC=110°,
综上,∠ADC的度数为125°或110°.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=ax2+bx+c(a≠0)的顶点坐标A(﹣1,3),与x轴的一个交点B(﹣4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a﹣b=0;②abc<0;③抛物线与x轴的另一个交点坐标是(3,0);④方程ax2+bx+c﹣3=0有两个相等的实数根;⑤当﹣4<x<﹣1时,则y2<y1.
其中正确的是( )

A. ①②③ B. ①③⑤ C. ①④⑤ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
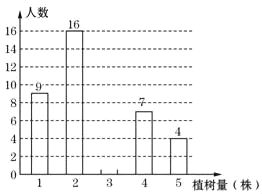
【题目】为了发展乡村旅游,建设美丽从化,某中学七年级一班同学都积极参加了植树活动,今年四月份该班同学的植树情况部分如图所示,且植树2株的人数占32%.
(1)求该班的总人数、植树株数的众数,并把条形统计图补充完整;
(2)若将该班同学的植树人数所占比例绘制成扇形统计图时,求“植树3株”对应扇形的圆心角的度数;
(3)求从该班参加植树的学生中任意抽取一名,其植树株数超过该班植树株数的平均数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=20 cm,AC=12 cm,点P从点B出发以每秒3 cm的速度向点A运动,点Q从点A出发以每秒2 cm的速度向点C运动,其中一个动点到达终点时,另一个动点也随之停止运动,当△APQ是以PQ为底边的等腰三角形时,运动的时间是 ( ).
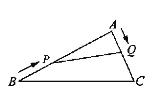
A. 2.5 sB. 3 sC. 3.5 sD. 4 s
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若△ABC的∠ABC=50°,∠ACB=70°,延长CB至点D,使BD=BA,延长BC至E点,使CE=CA, 连接AD、AE,则∠DAE的度数为__________度.
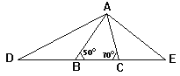
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】幻方是一种将数字排在正方形格子中,使每行、每列和每条对角线上的数字和都相等的模型.数学课上,老师在黑板上画出一个幻方如图所示,并设计游戏:一人将一颗能粘在黑板上的磁铁豆随机投入幻方内,另一人猜数,若所猜数字与投出的数字相符,则猜数的人获胜,否则投磁铁豆的人获胜.猜想的方法从以下两种中选一种:
|
|
|
|
|
|
|
|
|
![]() 猜“是大于
猜“是大于![]() 的数”或“不是大于
的数”或“不是大于![]() 的数”;
的数”;
![]() 猜“是
猜“是![]() 的倍数”或“不是
的倍数”或“不是![]() 的倍数”;
的倍数”;
如果轮到你猜想,那么为了尽可能获胜,你将选择哪--种猜数方法?怎么猜?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
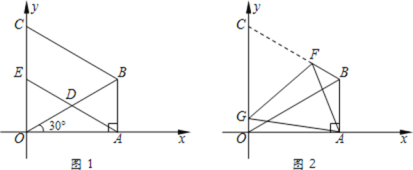
【题目】如图1,在△ABO中,∠OAB=90°,∠AOB=30°,OB=8.以OB为一边,在△OAB外作等边三角形OBC,D是OB的中点,连接AD并延长交OC于E.
(1)求点B的坐标;
(2)求证:四边形ABCE是平行四边形;
(3)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
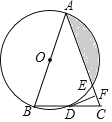
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作DF⊥AC于点F.
(1)若⊙O的半径为3,∠CDF=15°,求阴影部分的面积;
(2)求证:DF是⊙O的切线;
(3)求证:∠EDF=∠DAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
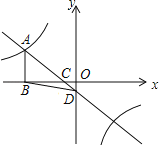
【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (a≠0)的图象在第二象限交于点A(m,2).与x轴交于点C(﹣1,0).过点A作AB⊥x轴于点B,△ABC的面积是3.
(a≠0)的图象在第二象限交于点A(m,2).与x轴交于点C(﹣1,0).过点A作AB⊥x轴于点B,△ABC的面积是3.
(1)求一次函数和反比例函数的解析式;
(2)若直线AC与y轴交于点D,求△BCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com