
【题目】如图,在△ABC中,AB=20 cm,AC=12 cm,点P从点B出发以每秒3 cm的速度向点A运动,点Q从点A出发以每秒2 cm的速度向点C运动,其中一个动点到达终点时,另一个动点也随之停止运动,当△APQ是以PQ为底边的等腰三角形时,运动的时间是 ( ).
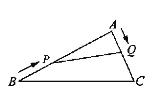
A. 2.5 sB. 3 sC. 3.5 sD. 4 s
科目:初中数学 来源: 题型:
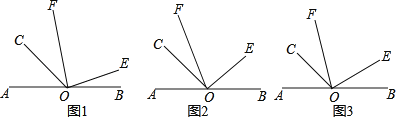
【题目】如图,O是直线AB上的一点,∠AOC=45°,OE是∠BOC内部的一条射线,且OF平分∠AOE.
(1)如图1,若∠COF=35°,求∠EOB的度数;
(2)如图2,若∠EOB=40°,求∠COF的度数;
(3)如图3,∠COF与∠EOB有怎样的数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有两个纸箱,每个纸箱内各装有4个材质、大小都相同的乒乓球,其中一个纸箱内4个小球上分别写有1、2、3、4这4个数,另一个纸箱内4个小球上分别写有5、6、7、8这4个数,甲、乙两人商定了一个游戏,规则是:从这两个纸箱中各随机摸出一个小球,然后把两个小球上的数字相乘,若得到的积是2的倍数,则甲得1分,若得到积是3的倍数,则乙得2分.完成一次游戏后,将球分别放回各自的纸箱,摇匀后进行下一次游戏,最后得分高者胜出.。
(1)请你通过列表(或树状图)分别计算乘积是2的倍数和3的倍数的概率;
(2)你认为这个游戏公平吗?为什么?若你认为不公平,请你修改得分规则,使游戏对双方公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
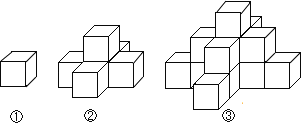
【题目】如图①是一个水平放置的小正方体木块,图②、图③是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,第四个叠放的图形时,小正方体木块总数应是___块;第七个叠放的图形时,小正方体木块总数应是____块.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
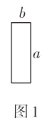
图1是一个长为![]() ,宽为
,宽为![]() 的长方形.现有相同的长方形若干,进行如下操作:
的长方形.现有相同的长方形若干,进行如下操作:
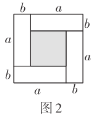
(1)用四块图1的小长方形不重叠地拼成一个如图2所示的正方形.请利用图2中阴影部分面积的不同表示方法,直接写出代数式![]() ,
,![]() ,
,![]() 之间的等量关系___________;
之间的等量关系___________;
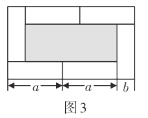
(2)将六块图1的小长方形不重叠地拼成一个如图3所示的长方形,通过不同方法计算阴影部分的面积,你能得到什么等式?请写出你的结论并用乘法法则证明这个等式成立;
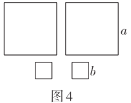
(3)现有图1的小长方形若干个,图4边长为![]() 的正方形两个,边长为
的正方形两个,边长为![]() 的正方形两个请你用这些图形拼成一个长方形(不重叠),使其面积为
的正方形两个请你用这些图形拼成一个长方形(不重叠),使其面积为![]() .画出你所拼成的长方形,并写出长方形的长和宽分别为多少.
.画出你所拼成的长方形,并写出长方形的长和宽分别为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 ,等腰三角形PEF中,PE=PF,点O在EF边上(异于点E,F),点Q是PO延长线上一点,若△EFQ为等腰三角形,则称点Q为△PEF的“同类点”.
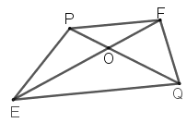
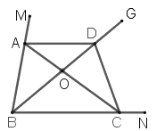
(1)如图,BG平分∠MBN,过射线BM上的点A作AD∥BN,交射线BG于点D,点O为BD上一点,连接AO并延长交射线BN于点C,若∠BAD=100°,∠BCD=70°,求证:点C是△ABD的“同类点”;
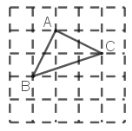
(2)如图③,在5×5的正方形网格图上有一个△ABC,点A,B,C均在格点上,在给出的网格图上有一个格点D,使得点D为△ABC的“同类点”,则这样的点D共有__________个;
(3)凸四边形ABCD中,∠ABC=110°,DA=AB=BC,对角线AC,BD交于点O,且BD≠CD,若点C为△ABD的“同类点”,请直接写出满足条件的∠ADC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
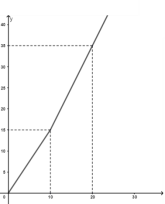
【题目】我国是世界上严重缺水的国家之一。为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费。即一月用水10吨以内(包括10吨)的用户,每吨收水费a元;一月用水超过10吨的用户,10吨水仍按每吨a元收费,超过10吨的部分,按每吨b元(b>a)收费。设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图所示。
(1)求a的值;某户居民上月用水8吨,应收水费多少元?
(2)求b的值,并写出当x>10时,y与x之间的函数关系式;
(3)已知居民甲上月比居民乙多用水4吨,两家共收水费46元,求他们上月分别用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
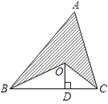
【题目】如图,在△ABC中,AB+AC=20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则图中阴影部分的面积等于______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com