
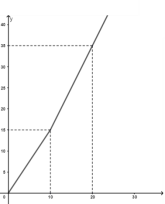
����Ŀ���ҹ�������������ȱˮ�Ĺ���֮һ��Ϊ����ǿ�����ˮ��ʶ��ij������ˮ��˾�Ծ�����ˮ�����Ի�Ϊ��λ�ֶμƷѰ취�շѡ���һ����ˮ10�����ڣ�����10�֣����û���ÿ����ˮ��aԪ��һ����ˮ����10�ֵ��û���10��ˮ��ÿ��aԪ�շѣ�����10�ֵIJ��֣���ÿ��bԪ��b>a)�շѡ���һ����������ˮx�֣�Ӧ��ˮ��yԪ��y��x֮��ĺ�����ϵ��ͼ��ʾ��
��1����a��ֵ��ij������������ˮ8�֣�Ӧ��ˮ�Ѷ���Ԫ��
��2����b��ֵ����д����x>10ʱ��y��x֮��ĺ�����ϵʽ��
��3����֪��������±Ⱦ����Ҷ���ˮ4�֣����ҹ���ˮ��46Ԫ�����������·ֱ���ˮ���ٶ֣�
���𰸡�(1)a=1.5,12Ԫ;(2)b=2,y=2x-5;(3) �������¼���ˮ16�֣�������������ˮ12��.
��������
��1����ͼ�п�֪��10��ˮ����15Ԫ����ôa=15��10=1.5Ԫ����ˮ8�֣�Ӧ��ˮ��1.5��8Ԫ��
��2����ͼ�п�֪��x��10ʱ����y=b��x-10��+15���ѣ�20��35������һ�κ�������ʽ���ɣ�
��3��Ӧ���жϳ�����ˮ�����ķ�Χ��
��1��a=15��10=1.5��
��8��ˮӦ��ˮ��8��1.5=12��Ԫ����
��2����x��10ʱ����y=b��x-10��+15��
��x=20��y=35���룬��35=10b+15��b=2��
�ʵ�x��10ʱ��y=2x-5��
��3�����������ˮ����������10�֣�ˮ�Ѳ�����46Ԫ�����������⣻
��������ˮ10�֣������ˮ14�֣�
��ˮ���ǣ�1.5��10+1.5��10+2��4��46�����������⣻
��ס�������������ˮ������10�֣�
��ס�������������ˮ�ֱ�Ϊx�֣�y�֣������ˮ��ˮ���ǣ�2x-5��Ԫ������ˮ��ˮ���ǣ�2y-5��Ԫ��
��![]()
��ã�![]()
�ʾ����������ˮ16�֣�������������ˮ12�֣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У�AD=3��CD=4����E��CD�ϣ���DE=1��



��1����֪����ͼ�٣�����AE������E��EF�AAE����BC�ڵ�F������AE����֤����ADE�ա�ECF������Ҫ֤������
��2��̽������ͼ�ڣ���P�ھ���ABCD�ı�AD�ϣ���P�����A��D�غϣ�������PE������E��EF��PE����BC�ڵ�F������PF����֤����PDE�͡�ECF���ƣ�
��3��Ӧ�ã���ͼ�ۣ���EF��AB�ڵ�F��EF�APE�������������䣬�ҡ�PEF�������6����AP�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB��20 cm��AC��12 cm����P�ӵ�B������ÿ��3 cm���ٶ����A�˶�����Q�ӵ�A������ÿ��2 cm���ٶ����C�˶�������һ�����㵽���յ�ʱ����һ������Ҳ��ֹ֮ͣ�˶�������APQ����PQΪ�ױߵĵ���������ʱ���˶���ʱ���� ( ).
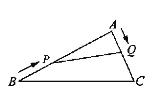
A. 2.5 sB. 3 sC. 3.5 sD. 4 s
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���÷���һ�ֽ��������������θ����У�ʹÿ�С�ÿ�к�ÿ���Խ����ϵ����ֺͶ���ȵ�ģ�ͣ���ѧ���ϣ���ʦ�ںڰ��ϻ���һ���÷���ͼ��ʾ���������Ϸ��һ�˽�һ����ճ�ںڰ��ϵĴ��������Ͷ��÷��ڣ���һ�˲�����������������Ͷ���������������������˻�ʤ������Ͷ���������˻�ʤ������ķ���������������ѡһ�֣�
|
|
|
|
|
|
|
|
|
![]() �¡��Ǵ���
�¡��Ǵ���![]() ���������Ǵ���
���������Ǵ���![]() ��������
��������
![]() �¡���
�¡���![]() �ı���������
�ı���������![]() �ı�������
�ı�������
����ֵ�����룬��ôΪ�˾����ܻ�ʤ���㽫ѡ����--�ֲ�����������ô�£�Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
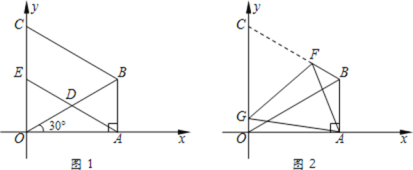
����Ŀ����ͼ1���ڡ�ABO�У���OAB��90�㣬��AOB��30�㣬OB��8����OBΪһ�ߣ��ڡ�OAB�����ȱ�������OBC��D��OB���е㣬����AD���ӳ���OC��E��
��1�����B�����ꣻ
��2����֤���ı���ABCE��ƽ���ı��Σ�
��3����ͼ2����ͼ1�е��ı���ABCO�۵���ʹ��C���A�غϣ��ۺ�ΪFG����OG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ŀǰ���ܵ��ڳ����ѻ����ռ���Ϊ��������������ij�̳��ƻ������ף������ֽ��ܵƹ�1200ֻ�������ֽ��ܵƵĽ��ۡ�������±���
���ۣ�Ԫ/ֻ�� | ��ۣ�Ԫ/ֻ�� | |
���� | 25 | 40 |
���� | 45 | 60 |
��1����ν������ܱ�֤������ǡ��Ϊ46000Ԫ��
��2������ǡ����һ���̳����������������ͽ��ܵƴ�����ۣ�����������ѧ��֪ʶԤ��һ�¼��ͽ��ܵ�Ҫ���۲���ʹ�������������9200Ԫ�����������������أ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
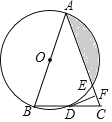
����Ŀ����ͼ������ABC�У�AB=AC����ABΪֱ���ġ�O�ֱ���BC��AC���ڵ�D��E������D��DF��AC�ڵ�F��
��1������O�İ뾶Ϊ3����CDF=15��������Ӱ���ֵ������
��2����֤��DF�ǡ�O�����ߣ�
��3����֤����EDF=��DAC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A(��t��0)��B(0��t)������t��0����CΪOA��һ�㣬OD��BC�ڵ�D���ҡ�BCO=45������COD
(1) ��֤��BCƽ�֡�ABO
(2) ��![]() ��ֵ
��ֵ
(3) ����PΪ����������һ���㣬�ҡ�APO=135��������AP��BP�Ƿ����ij��ȷ����λ�ù�ϵ��˵������
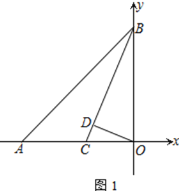
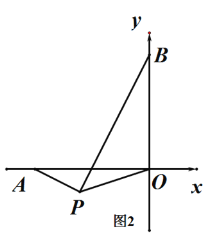
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABC�У�AB��AC����ABC��35�㣬E��BC����һ����AE��CE��D��
BC���ϵ��е㣬����AD��AE��
��1�����DAE�Ķ�����
��2����BD�ϴ��ڵ�F���ҡ�AFE����AEF����֤��BF��CE��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com