
【题目】如图,等腰△ABC中,AB=AC,∠ABC=35°,E是BC边上一点且AE=CE,D是
BC边上的中点,连接AD,AE.
(1)求∠DAE的度数;
(2)若BD上存在点F,且∠AFE=∠AEF,求证:BF=CE.

【答案】(1)∠DAE=20°;(2)见解析
【解析】
(1)根据等边对等角和已知∠ABC的度数可求得∠CAE的度数,再根据等腰三角形三线合一的性质可得AD⊥BC,然后根据直角三角形的性质可求出∠DAC的度数,进一步即可求出结果;
(2)先根据等角对等边得到AF=AE,再根据等腰三角形三线合一的性质得FD=ED,进一步即得结论.
解:(1)∵AB=AC,∠ABC=35°,∴∠C=35°,
∵AE=CE,∴∠CAE=∠C=35°,
∵D是BC边上的中点,∴AD⊥BC,∴∠ADC=90°,
∴∠DAC=90°﹣35°=55°,
∴∠DAE=∠DAC﹣∠CAE=55°﹣35°=20°;
(2)证明:∵∠AFE=∠AEF,∴AF=AE,
∵AD⊥BC,∴D是EF边上的中点,∴FD=ED,
∵D是BC边上的中点,∴BD=CD,
∴BD﹣FD=CD﹣ED,即BF=CE.


科目:初中数学 来源: 题型:
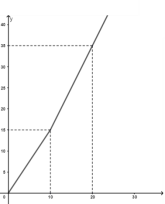
【题目】我国是世界上严重缺水的国家之一。为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费。即一月用水10吨以内(包括10吨)的用户,每吨收水费a元;一月用水超过10吨的用户,10吨水仍按每吨a元收费,超过10吨的部分,按每吨b元(b>a)收费。设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图所示。
(1)求a的值;某户居民上月用水8吨,应收水费多少元?
(2)求b的值,并写出当x>10时,y与x之间的函数关系式;
(3)已知居民甲上月比居民乙多用水4吨,两家共收水费46元,求他们上月分别用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
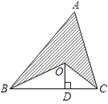
【题目】如图,在△ABC中,AB+AC=20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则图中阴影部分的面积等于______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算并观察下列各式:
(x1)(x1) ;
(x1)( ![]() x1) ;
x1) ;
(x1)( ![]()
![]() x1) ;
x1) ;
(2)从上面的算式及计算结果,你发现了什么?请根据你发现的规律直接写下面的空格.(x1) ![]() 1;
1;
(3)利用你发现的规律计算:![]() ;
;
(4)利用该规律计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
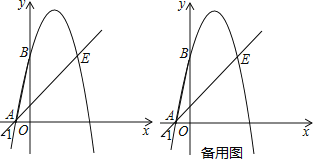
【题目】如图,抛物线y=ax2+4x+c(a≠0)经过点A(﹣1,0),点E(4,5),与y轴交于点B,连接AB.
(1)求该抛物线的解析式;
(2)将△ABO绕点O旋转,点B的对应点为点F.
①当点F落在直线AE上时,求点F的坐标和△ABF的面积;
②当点F到直线AE的距离为![]() 时,过点F作直线AE的平行线与抛物线相交,请直接写出交点的坐标.
时,过点F作直线AE的平行线与抛物线相交,请直接写出交点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
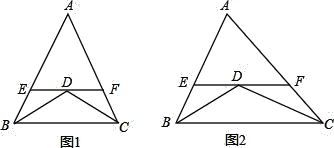
【题目】(1)如图1,已知:在△ABC中,AB=AC=10,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,分别交AB、AC于E、F两点,则图中共有__________个等腰三角形;EF与BE、CF之间的数量关系是__________,△AEF的周长是__________;
(2)如图2,若将(1)中“△ABC中,AB=AC=10”该为“若△ABC为不等边三角形,AB=8,AC=10”其余条件不变,则图中共有__________个等腰三角形;EF与BE、CF之间的数量关系是什么?证明你的结论,并求出△AEF的周长;
(3)已知:如图3,D在△ABC外,AB>AC,且BD平分∠ABC,CD平分△ABC的外角∠ACG,过点D作DE∥BC,分别交AB、AC于E、F两点,则EF与BE、CF之间又有何数量关系呢?直接写出结论不证明.
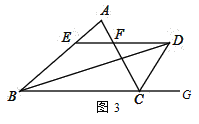
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1+∠4﹦180°,∠2﹦∠E,则EF∥BC,下面是王华同学的推导过程﹐请你帮他在括号内填上推导依据或内容.
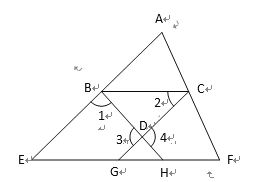
证明:
∵∠1+∠4﹦180°( ),
∠3﹦∠4 ( ),
∴∠1﹢ ﹦180°.
∴AE∥CG ( )
∴∠E﹦∠CGF( ).
∵∠2﹦∠E(已知)
∴ ∠2﹦∠CGF( ).
∴ BC∥EF( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com