
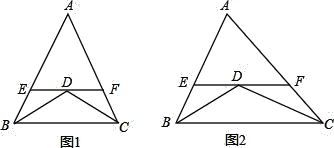
ЁОЬтФПЁПЃЈ1ЃЉШчЭМ1ЃЌвбжЊЃКдкЁїABCжаЃЌAB=AC=10ЃЌBDЦНЗжЁЯABCЃЌCDЦНЗжЁЯACBЃЌЙ§ЕуDзїEFЁЮBCЃЌЗжБ№НЛABЁЂACгкEЁЂFСНЕуЃЌдђЭМжаЙВга__________ИіЕШбќШ§НЧаЮЃЛEFгыBEЁЂCFжЎМфЕФЪ§СПЙиЯЕЪЧ__________ЃЌЁїAEFЕФжмГЄЪЧ__________ЃЛ
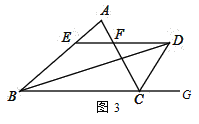
ЃЈ2ЃЉШчЭМ2ЃЌШєНЋЃЈ1ЃЉжаЁАЁїABCжаЃЌAB=AC=10ЁБИУЮЊЁАШєЁїABCЮЊВЛЕШБпШ§НЧаЮЃЌAB=8ЃЌAC=10ЁБЦфгрЬѕМўВЛБфЃЌдђЭМжаЙВга__________ИіЕШбќШ§НЧаЮЃЛEFгыBEЁЂCFжЎМфЕФЪ§СПЙиЯЕЪЧЪВУДЃПжЄУїФуЕФНсТлЃЌВЂЧѓГіЁїAEFЕФжмГЄЃЛ
ЃЈ3ЃЉвбжЊЃКШчЭМ3ЃЌDдкЁїABCЭтЃЌAB>ACЃЌЧвBDЦНЗжЁЯABCЃЌCDЦНЗжЁїABCЕФЭтНЧЁЯACGЃЌЙ§ЕуDзїDEЁЮBCЃЌЗжБ№НЛABЁЂACгкEЁЂFСНЕуЃЌдђEFгыBEЁЂCFжЎМфгжгаКЮЪ§СПЙиЯЕФиЃПжБНгаДГіНсТлВЛжЄУїЃЎ
ЁОД№АИЁПЃЈ1ЃЉ5ЃЛBE+CF=EFЃЛ20ЃЛ ЃЈ2ЃЉ2ЃЛBE+CF=EFЃЌжЄУїМћНтЮіЃЛЁїAEFЕФжмГЄ=18ЃЛЃЈ3ЃЉBE-CF=EFЃЌРэгЩМћНтЮі.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнНЧЦНЗжЯпЕФЖЈвхПЩЕУЁЯEBD=ЁЯCBDЃЌЁЯFCD=ЁЯBCDЃЌдйИљОнСНжБЯпЦНааЃЌФкДэНЧЯрЕШПЩЕУЁЯEDB=ЁЯCBDЃЌЁЯFDC=ЁЯBCDЃЌШЛКѓЧѓГіЁЯEBD=ЁЯEDBЃЌЁЯFDC=ЁЯBCDЃЌдйИљОнЕШНЧЖдЕШБпПЩЕУBE=DEЃЌCF=DFЃЌШЛКѓНтД№МДПЩЃЛ
ЃЈ2ЃЉИљОнНЧЦНЗжЯпЕФЖЈвхПЩЕУЁЯEBD=ЁЯCBDЃЌЁЯFCD=ЁЯBCDЃЌдйИљОнСНжБЯпЦНааЃЌФкДэНЧЯрЕШПЩЕУЁЯEDB=ЁЯCBDЃЌЁЯFDC=ЁЯBCDЃЌШЛКѓЧѓГіЁЯEBD=ЁЯEDBЃЌЁЯFDC=ЁЯBCDЃЌдйИљОнЕШНЧЖдЕШБпПЩЕУBE=DEЃЌCF=DFЃЌШЛКѓНтД№МДПЩЃЛ
ЃЈ3ЃЉгЩЃЈ2ЃЉжЊBE=EDЃЌCF=DFЃЌШЛКѓРћгУЕШСПДњЛЛМДПЩжЄУїBEЁЂCFЁЂEFгадѕбљЕФЪ§СПЙиЯЕЃЎ
ЪдЬтНтЮіЃКНтЃКЃЈ1ЃЉBE+CF=EFЃЎРэгЩШчЯТЃК
ЁпAB=ACЃЌЁрЁЯABC=ЁЯACBЃЎЁпBDЦНЗжЁЯABCЃЌCDЦНЗжЁЯACBЃЌЁрЁЯEBD=ЁЯCBDЃЌЁЯFCD=ЁЯBCDЃЌЁрЁЯDBC=ЁЯDCBЃЌЁрDB=DCЃЎ
ЁпEFЁЮBCЃЌЁрЁЯAEF=ЁЯABCЃЌЁЯAFE=ЁЯACBЃЌЁЯEDB=ЁЯCBDЃЌЁЯFDC=ЁЯBCDЃЌЁрЁЯEBD=ЁЯEDBЃЌЁЯFDC=ЁЯBCDЃЌЁрBE=DEЃЌCF=DFЃЌAE=AFЃЌЁрЕШбќШ§НЧаЮгаЁїABCЃЌЁїAEFЃЌЁїDEBЃЌЁїDFCЃЌЁїBDCЙВ5ИіЃЌЁрBE+CF=DE+DF=EFЃЌМДBE+CF=EFЃЌЁїAEFЕФжмГЄ=AE+EF+AF=AE+BE+AF+FC=AB+AC=20ЃЎ
ЙЪД№АИЮЊЃК5ЃЛBE+CF=EFЃЛ20ЃЛ
ЃЈ2ЃЉBE+CF=EFЃЎЁпBDЦНЗжЁЯABCЃЌCDЦНЗжЁЯACBЃЌЁрЁЯEBD=ЁЯCBDЃЌЁЯFCD=ЁЯBCDЃЎЁпEFЁЮBCЃЌЁрЁЯEDB=ЁЯCBDЃЌЁЯFDC=ЁЯBCDЃЌЁрЁЯEBD=ЁЯEDBЃЌЁЯFDC=ЁЯBCDЃЌЁрBE=DEЃЌCF=DFЃЌЁрЕШбќШ§НЧаЮгаЁїBDEЃЌЁїCFDЃЌЁрBE+CF=DE+DF=EFЃЌМДBE+CF=EFЃЎЁїAEFЕФжмГЄ=AE+EF+AF=AE+ED+DF+AF=AE+EB+CF+AF=AB+AC=8+10=18ЃЎ
ДЫЪБгаСНИіЕШбќШ§НЧаЮЃЌEFЃНBEЃЋCFЃЌCЁїAEFЃН18ЃЎ
ЃЈ3ЃЉBEЉCF=EFЃЎгЩЃЈ1ЃЉжЊBE=EDЃЎЁпEFЁЮBCЃЌЁрЁЯEDC=ЁЯDCG=ЁЯACDЃЌЁрCF=DFЃЎгжЁпEDЉDF=EFЃЌЁрBEЉCF=EFЃЎ


 КьЙћзгШ§МЖВтЪдОэЯЕСаД№АИ
КьЙћзгШ§МЖВтЪдОэЯЕСаД№АИ ПЮЬУСЗМгВтЯЕСаД№АИ
ПЮЬУСЗМгВтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋЯТСажЄУїЙ§ГЬВЙГфЭъећЃК
вбжЊЃКШчЭМЃЌЕуB.EЗжБ№дкACЁЂDFЩЯЃЌAFЗжБ№НЛBDЁЂCEгкЕуMЁЂNЃЌЁЯ1=ЁЯ2ЃЌЁЯA=ЁЯF.
ЧѓжЄЃКЁЯC=ЁЯD.

жЄУїЃКвђЮЊЁЯ1=ЁЯ2(вбжЊ).
гжвђЮЊЁЯ1=ЁЯANC(______)ЃЌ
Ыљвд______(ЕШСПДњЛЛ).
Ыљвд______ЁЮ______(ЭЌЮЛНЧЯрЕШЃЌСНжБЯпЦНаа).
ЫљвдЁЯABD=ЁЯC(______).
гжвђЮЊЁЯA=ЁЯF(вбжЊ)ЃЌ
Ыљвд______ЁЮ______(______).
Ыљвд______(СНжБЯпЦНааЃЌФкДэНЧЯрЕШ).
ЫљвдЁЯC=ЁЯD(______).
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁїABCжаЃЌADЁЭBCЃЌAEЦНЗжЁЯBACНЛBCгкЕуEЃЎ
ЃЈ1ЃЉЁЯB=30ЁуЃЌЁЯC=70ЁуЃЌЧѓЁЯEADЕФДѓаЁЃЎ
ЃЈ2ЃЉШєЁЯBЃМЁЯCЃЌдђ2ЁЯEADгыЁЯC-ЁЯBЪЧЗёЯрЕШЃПШєЯрЕШЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЪЬтЧщОАЃКШчЭМ1ЃЌABЁЮCDЃЌЁЯPAB=140ЁуЃЌЁЯPCD=135ЁуЃЌЧѓЁЯAPCЕФЖШЪ§ЃЎ
ЃЈ1ЃЉРіРіЭЌбЇПДЙ§ЭМаЮКѓСЂМДПкД№ГіЃКЁЯAPC=85ЁуЃЌЧыФуВЙШЋЫ§ЕФЭЦРэвРОнЃЎ
ШчЭМ2ЃЌЙ§ЕуPзїPEЁЮABЃЌ
ЁпABЁЮCDЃЌЁрPEЁЮCDЃЎ ЃЈЁЁ ЁЁЃЉ
ЁрЁЯA+ЁЯAPE=180ЁуЃЎ
ЁЯC+ЁЯCPE=180ЁуЃЎ ЃЈЁЁ ЁЁЃЉ
ЁпЁЯPAB=140ЁуЃЌЁЯPCD=135ЁуЃЌ
ЁрЁЯAPE=40ЁуЃЌЁЯCPE=45Ёу
ЁрЁЯAPC=ЁЯAPE+ЁЯCPE=85ЁуЃЎЃЈЁЁ ЁЁЃЉ
ЮЪЬтЧЈвЦЃК
ЃЈ2ЃЉШчЭМ3ЃЌADЁЮBCЃЌЕБЕуPдкAЁЂBСНЕужЎМфдЫЖЏЪБЃЌЁЯADP=ЁЯІСЃЌЁЯBCP=ЁЯІТЃЌЧѓЁЯCPDгыЁЯІСЁЂЁЯІТжЎМфгаКЮЪ§СПЙиЯЕЃПЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШчЙћЕуPдкAЁЂBСНЕуЭтВрдЫЖЏЪБЃЈЕуPгыЕуAЁЂBЁЂOШ§ЕуВЛжиКЯЃЉЃЌЧыФужБНгаДГіЁЯCPDгыЁЯІСЁЂЁЯІТжЎМфЕФЪ§СПЙиЯЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЁЮCDЃЌEЮЊACЩЯвЛЕуЃЌЁЯABEЃНЁЯAEBЃЌЁЯCDEЃНЁЯCEDЃЎ
ЧѓжЄЃКBEЁЭDEЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкОиаЮABCDжаЃЌAB=4ЃЌBC=3ЃЌЕуPдкABЩЯЃЎШєНЋЁїDAPбиDPелЕўЃЌЪЙЕуAТфдкОиаЮЖдНЧЯпЩЯЕФAЁфДІЃЌдђAPЕФГЄЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁЧПгыаЁИеЖМзЁдкАВПЕаЁЧјЃЌдкЭЌвЛЫљбЇаЃЖСЪщЃЎФГЬьдчЩЯЃЌаЁЧП![]() ДгАВПЕаЁЧјеОГЫзјаЃГЕШЅбЇаЃЃЌЭОжаашЭЃППСНИіеОЕуВХФмЕНДябЇаЃеОЕуЃЌЧвУПИіеОЕуЭЃСє
ДгАВПЕаЁЧјеОГЫзјаЃГЕШЅбЇаЃЃЌЭОжаашЭЃППСНИіеОЕуВХФмЕНДябЇаЃеОЕуЃЌЧвУПИіеОЕуЭЃСє![]() ЗжжгЃЌаЃГЕааЪЛЭОжаЪМжеБЃГждШЫйЃЎЕБЬьдчЩЯЃЌаЁИе
ЗжжгЃЌаЃГЕааЪЛЭОжаЪМжеБЃГждШЫйЃЎЕБЬьдчЩЯЃЌаЁИе![]() ДгАВПЕаЁЧјеОГЫзјГізтГЕбиЯрЭЌТЗЯпГіЗЂЃЌГізтГЕдШЫйааЪЛЃЌБШаЁЧПГЫзјЕФаЃГЕдч
ДгАВПЕаЁЧјеОГЫзјГізтГЕбиЯрЭЌТЗЯпГіЗЂЃЌГізтГЕдШЫйааЪЛЃЌБШаЁЧПГЫзјЕФаЃГЕдч![]() ЗжжгЕНбЇаЃеОЕуЃЎЫћУЧГЫзјЕФГЕСОДгАВПЕаЁЧјеОГіЗЂЫљааЪЛТЗГЬ
ЗжжгЕНбЇаЃеОЕуЃЎЫћУЧГЫзјЕФГЕСОДгАВПЕаЁЧјеОГіЗЂЫљааЪЛТЗГЬ![]() ЃЈЧЇУзЃЉгыааЪЛЪБМф
ЃЈЧЇУзЃЉгыааЪЛЪБМф![]() ЃЈЗжжгЃЉжЎМфЕФКЏЪ§ЭМЯѓШчЭМЫљЪОЃЎ
ЃЈЗжжгЃЉжЎМфЕФКЏЪ§ЭМЯѓШчЭМЫљЪОЃЎ
ЃЈ1ЃЉЧѓЕу![]() ЕФзнзјБъ
ЕФзнзјБъ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉаЁИеГЫзјГізтГЕГіЗЂКѓОЙ§ЖрЩйЗжжгзЗЕНаЁЧПЫљГЫзјЕФаЃГЕЃПВЂЧѓДЫЪБЫћУЧОрбЇаЃеОЕуЕФТЗГЬЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌBDЁЮGEЃЌAQ ЦНЗжЁЯFACЃЌНЛ BD гк QЃЌЁЯGFA=50ЁуЃЌЁЯQ=25ЁуЃЌдђЁЯACB ЕФ ЖШЪ§ЃЈ ЃЉ
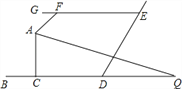
A. 90Ёу B. 95Ёу C. 100Ёу D. 105Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвУЧИјГіШчЯТЖЈвхЃКШєвЛИіЫФБпаЮжаДцдкЯрСкСНБпЕФЦНЗНКЭЕШгквЛЬѕЖдНЧЯпЕФЦНЗНЃЌдђГЦетИіЫФБпаЮЮЊЙДЙЩЫФБпаЮЃЌетСНЬѕЯрСкЕФБпГЦЮЊетИіЫФБпаЮЕФЙДЙЩБпЃЎ
(1)ШчЭМЂйЃЌвбжЊИёЕу(аЁе§ЗНаЮЕФЖЅЕу)O(0ЃЌ0)ЃЌA(3ЃЌ0)ЃЌB(0ЃЌ4)ЃЌЧыФуЛГівдИёЕуЮЊЖЅЕуЃЌOAЃЌOBЮЊЙДЙЩБпЧвЖдНЧЯпЯрЕШЕФЙДЙЩЫФБпаЮOAMBЃЛ
 ЁЁЁЁ
ЁЁЁЁ
(2)ШчЭМЂкЃЌНЋЁїABCШЦЖЅЕуBАДЫГЪБеыЗНЯђа§зЊ60ЁуЃЌЕУЕНЁїDBEЃЌСЌНгADЃЌDCЃЌЁЯDCBЃН30ЁуЃЌЧѓжЄЃКDC2ЃЋBC2ЃНAC2ЃЌМДЫФБпаЮABCDЪЧЙДЙЩЫФБпаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com