
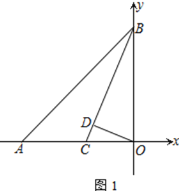
【题目】如图,A(-t,0)、B(0,t),其中t>0,点C为OA上一点,OD⊥BC于点D,且∠BCO=45°+∠COD
(1) 求证:BC平分∠ABO
(2) 求![]() 的值
的值
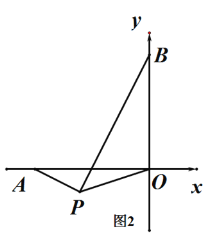
(3) 若点P为第三象限内一动点,且∠APO=135°,试问AP和BP是否存在某种确定的位置关系?说明理由
【答案】(1)见解析;(2)2;(3)BP⊥AP,理由见解析;
【解析】
(1)分别证明:∠ABC=∠DOC,∠CBO=∠DOC即可.
(2)在BC上截DE=DO,证CE=OE=BE,则E为BC的中点,则BC=2EC=2(DE+DC)=2(OD+CD),代入化简即可,也可以用四点共圆去思考更加简单.
(3)作OM⊥OP交PB于M,交AP的延长线于N,在证明△BOP≌△AON,即可解答.
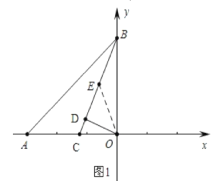
(1)证明:如图1中,∵AO=BO=t,∠AOB=90°,
∴∠OAB=∠OBA=45°,
∵∠BCO=45°+∠COD=∠BAO+∠ABC,
∴∠COD=∠ABC,
∵OD⊥BC,
∴∠CDO=90°,
∵∠DOC+∠DCO=90°,∠CBO+∠BCO=90°,
∴∠DOC=∠CBO,
∴∠ABC=∠CBO.
(2)中图1中,作DE=DO,
∵∠ODE=90°,
∴∠DEO=45°=∠EBO+∠EOB,
∵∠ABC=∠CBO=![]() ∠ABO=22.5°,
∠ABO=22.5°,
∴∠EOB=∠EBO=22.5°,
∴EB=EO,
∵∠ECO=∠EOC=67.5°,
∴EC=EO,
∴BC=2EC=2(DE+CD)=2OD+2CD,
∴![]() =2.
=2.
(3)结论:BP⊥AP,如图2,理由如下:
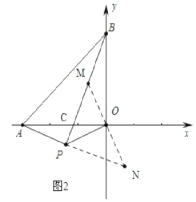
作OM⊥OP交PB于M,交AP的延长线于N,
∵∠APO=135°,
∴∠OPN=∠N=45°,
∴OP=ON,
∵∠AOB=∠PON=90°,
∴∠BOP=∠AON,
在△OBP和△OAN中,
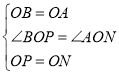 ,
,
∴△BOP≌△AON,
∴∠BPO=∠N=45°,
∵∠OPN=45°,
∴∠BPN=∠BPO+∠OPN=90°,
∴BP⊥AP.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
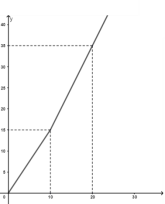
【题目】我国是世界上严重缺水的国家之一。为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费。即一月用水10吨以内(包括10吨)的用户,每吨收水费a元;一月用水超过10吨的用户,10吨水仍按每吨a元收费,超过10吨的部分,按每吨b元(b>a)收费。设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图所示。
(1)求a的值;某户居民上月用水8吨,应收水费多少元?
(2)求b的值,并写出当x>10时,y与x之间的函数关系式;
(3)已知居民甲上月比居民乙多用水4吨,两家共收水费46元,求他们上月分别用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上![]() ,
,![]() 两点对应的有理数分别为
两点对应的有理数分别为![]() 和12,点
和12,点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度沿数轴负方向运动,点
出发,以每秒1个单位长度的速度沿数轴负方向运动,点![]() 同时从点
同时从点![]() 出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为
出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为![]() 秒.
秒.
![]()
(1)求经过2秒后,数轴点![]() 、
、![]() 分别表示的数;
分别表示的数;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)在运动过程中是否存在时间![]() 使
使![]() ,若存在,请求出此时
,若存在,请求出此时![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠1=∠2,点G为AD的中点,连接BG并延长,交AC于点E,F为AB上一点,且CF⊥AD于点H,下列判断中:①AD是△ABE的角平分线;②BE是△ABD边AD上的中线;③CH是△ACD边AD上的高.正确的个数有( )
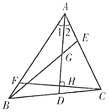
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB+AC=20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则图中阴影部分的面积等于______.
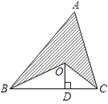
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算并观察下列各式:
(x1)(x1) ;
(x1)( ![]() x1) ;
x1) ;
(x1)( ![]()
![]() x1) ;
x1) ;
(2)从上面的算式及计算结果,你发现了什么?请根据你发现的规律直接写下面的空格.(x1) ![]() 1;
1;
(3)利用你发现的规律计算:![]() ;
;
(4)利用该规律计算:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com